Социометрическая матрица.

Ф.И.О.	Иванов	Петров	Сидоров	…	ВС	ОС	ОВ	ОО
Иванов		2	()
Петров	1
Сидоров	3	()		1 2
Обозначение показателей
ВП	2	1	0
ОП
ОВ
ОС
ВВ
ВО

В итоговых нижних строках и правых столбцах используются следующие обозначения:

• ВС – количество выборов, сделанных данным человеком;
• ОС – количество отклонений, сделанных данным человеком;
• ВП – сумма выборов, полученных данным человеком;
• ОП – сумма отклонений, полученных данным человеком;
• ОВ – количество ожидаемых выборов;
• ОО – количество ожидаемых отклонений;
• ВВ – количество взаимных выборов;
• ВО – количество взаимных отклонений.

В нижние строки матрицы заносятся результаты о количестве полученных выборов (независимо, в какую очередь – 1, 2, 3-ю) и отклонений, о количестве взаимных выборов и отклонений, о количестве ожидаемых от данного лица выборов и отклонений.

В крайние правые столбцы матрицы заносятся результаты о количестве сделанных выборов и отклонений, о количестве ожидаемых данным лицом выборов и отклонений.

Число выборов, полученных каждым человеком, является мерилом положения его в системе личных отношений, измеряет его «социометрический статус». Люди, которые получают наибольшее количество выборов, пользуются наибольшей популярностью, симпатией, их именуют «звездами». Обычно к группе «звезд» по числу полученных выборов относят тех, кто получает 6 и более выборов (если, по условиям опыта каждый член группы делал 3 выбора). Если человек получает среднее число выборов, его относят к категории «предпочитаемых», если меньше среднего числа выборов (1-2 выбора), то к категории «пренебрегаемых», если не получил ни одного выбора, то к категории «изолированных», если получил только отклонения – то к категории «отвергаемых».

С целью более достоверного выделения «звезд» и «пренебрегаемых» используют некоторые методы статистического анализа. В ходе статистического анализа полученного первичного материала устанавливают критические значения количества выборов, границы доверительного интервала, за пределами которого полученные выборы можно считать статистически достоверными. Эмпирические кривые распределения выборов часто асимметричны и апроксимируются биноминальным законом распределения. Экспериментальная ситуация социометрического обследования весьма близка к ситуации последовательных дихотомических выборов.

Формулы расчёта

Верхняя и нижняя критические границы рассчитываются по следующей общей формуле:

где Х – критическое значение количества V(М) выборов; t – поправочный коэффициент, учитывающий отклонение эмпирического распределения от теоретического; b – среднее отклонение; M – среднее количество выборов, приходящихся на одного человека.

Коэффициент t определяется по специальной таблице на основе предварительного вычисления другого коэффициента О_D свидетельствующего о степени отклонения распределения выборов от случайного:

где p – оценка вероятности быть выбранным в данной группе; q – оценка вероятности оказатьcя отвергнутым в данной группе; b – отклонение количества полученных индивидами выборов от среднего их числа, приходящегося на одного члена группы;

p и q, в свою очередь, определяются при помощи следующих формул:

,

где N – количество участников в группе; M– среднее количество выборов, полученных одним участником.

M вычисляется при помощи формулы:

где d – общее количество выборов, сделанных членами данной группы.

b определяется по формуле:

Пример процедуры расчётов

Проиллюстрируем процедуру расчетов. Исследовали группу в 31 человек, участники которой в общей сложности сделали 270 выборов. Найдем среднее количество выборов, приходящихся на одного человека в группе:

Определим оценку вероятности быть избранным в данной группе:

Вычислим среднее квадратное отклонение:

Подсчитаем коэффициент асимметричности:

Теперь по таблице определим величину t отдельно для правой и левой частей распределения. В левой части таблицы приведены значения для нижней границы доверительного интервала, а в правой – для верхней. Для обеих границ (верхней и нижней) значения даны для трех различных вероятностей допустимой ошибки:

; ; ;

Таблица значений коэффициента асимметричности по Сальвосу

Коэффициент асимметричности ОD	Вероятность ошибки p	Коэффициент асимметричности ОD	Вероятность ошибки p
0,05	0,01	0,001	0,05	0,01	0,001
0,0	-1,64	-2,33	-3,09	0,0	1,64	2,33	3,09
0,1	-1,62	-2,25	-2,95	0,1	1,67	2,40	3,23
0,2	-1,59	-2,18	-2,81	0,2	1,70	2,47	3,38
0,3	-1,56	-2,10	-2,67	0,3	1,73	2,54	3,52
0,4	-1,52	-2,03	-2,53	0,4	1,75	2,62	3,67
0,5	-1,49	-1,95	-2,40	0,5	1,77	2,69	3,81
0,6	-1,46	-1,88	-2,27	0,6	1,80	2,76	3,96
0,7	-1,42	-1,81	-2,14	0,7	1,82	2,83	4,10
0,8	-1,39	-1,73	-2,00	0,8	1,84	2,89	4,24
0,9	-1,35	-1,66	-1,90	0,9	1,86	2,96	4,39
1,0	-1,32	-1,59	-1,79	1,0	1,88	3,02	4,53
1,1	-1,28	-1,52	-1,68	1,1	1,89	3,09	4,67

Поскольку в таблице нет значения, равного 0,16, а есть только значения 0,1 и 0,2, то выберем поправочные коэффициенты, находящиеся между этими табличными значениями.

Для О_D=0,1 поправочный коэффициент составит (-1,62), а для О_D=0,2 – (-1,59). С учетом того, что реальное значение О_D=0,16, возьмем поправочный коэффициент t промежуточного значения и примем его равным (-1,60) (левая половина таблицы).

Проделав подобную операцию и в правой части таблицы, получим второй поправочный коэффициент 1,69, величина которого расположена между табличными значениями для О_D=0,1 и О_D=0,2. Верхнюю критическую границу вычислим, подставив в формулу значение t из правой части таблицы: X_верхн = 9,0 + 1,69 х 2,51 = 13,24.

Для определения нижней границы доверительного интервала используем значение t, взятое из левой части таблицы: Х_нижн = 9,0 – 1,6 x 2,51 = 4,98.

В связи с тем, что количество полученных выборов – это всегда целое число, округлим полученные значения до целых чисел.

Теперь можно сделать вывод, что все испытуемые изученной группы, получившие 14 и более выборов, имеют высокий социометрический статус, являются «звездами», а испытуемые, получившие 4 и меньше выборов, – низкий статус, причем, утверждая это, допускаем ошибку не более 5 %.

Если допускать ошибку в 1 %, то из таблицы значения t берем иные:

X_верхн = 9,0 + 3,32 х 2,51 = 17,33; Х_нижн = 9,0 – 2,84 x 2,51 = 1,87.

Округлим до целых чисел: X_верхн = 18; Х_нижн = 1. Таким образом, допуская ошибку не более, чем на 1 %, можно утверждать, что лидерами являются только те, кто получил не менее 18 выборов, а низкий статус – у испытуемых, получивших меньше двух выборов.

Анализ социоматрицы по каждому критерию дает достаточно наглядную картину взаимоотношений в группе. Могут быть построены суммарные социоматрицы, дающие картину выборов по нескольким критериям, а также социоматрицы по данным межгрупповых выборов.

Основное достоинство социоматрицы – возможность представить выборы в числовом виде, что в свою очередь позволяет проранжировать порядок влияний в группе. На основе социоматрицы строится социограмма – карта социометрических выборов (социометрическая карта), производится расчет социометрических индексов.

Социоматрица - это матрица связей, с помощью которой анализируются внутриколлективные отношения. В социоматрицу в форме числовых значений и символов заносится информация, полученная в ходе опроса.

Анализ социоматрицы по каждому критерию дает достаточно наглядную картину взаимоотношений в группе. Могут быть построены суммарные социоматрицы, дающие картину выборов по нескольким критериям, а также социоматрицы по данным межгрупповых выборов.

Основное достоинство социоматрицы – возможность представить выборы в числовом виде, что в свою очередь позволяет проранжировать порядок влияний в группе. На основе социоматрицы строится социограмма – карта социометрических выборов (социометрическая карта), производится расчет социометрических индексов.
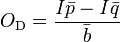
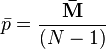
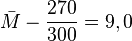
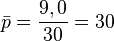
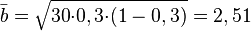
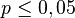