Формула полной вероятности. Пусть событие А может быть реализовано только при условии появления одного из событий Hi, i = 1,
Пусть событие А может быть реализовано только при условии появления одного из событий Hi, i = 1,..., n. Предположим, что события Hi несовместны, образуют полную группу (т.е. в результате испытания непременно произойдет одно из них) и вероятности их до опыта известны.. Такие события Hi называются гипотезами. Тогда вероятность события А можно вычислить с помощью формулы полной вероятности: . Задача 5. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студента, а третий — 21 студентов (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, зато у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен. Решение. Обозначим через
Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда снова в силу условия задачи
По формуле полной вероятности получаем:
Для решения задач такое типа удобно использовать так называемое "дерево" вероятностей. Из формулы полной вероятности следует, что для вычисления вероятности события А необходимо осуществить перебор всех путей, ведущих к результирующему событию А; вычислить и расставить на соответствующих путях вероятности Р(Нi) того, что движение будет происходить по данному пути, и вероятности Р(А/ Нi) того, что на данном пути будет достигнуто конечное событие А. Затем вероятности, стоящие на одном пути, перемножаются, а результаты, полученные для различных путей, складываются. Каждое из условий может в свою очередь делиться на несколько дополнительных условий или гипотез, т.е. на каждом этапе оно допускает неограниченное число ветвлений схемы, поэтому в решении задач удобнее пользоваться не самой формулой полной вероятности, а графической схемой полной вероятности, которую называют "деревом" вероятностей.
|

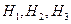 – гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи
– гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи ,
,  ,
,  .
. ,
,  ,
, 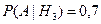 .
. .
.


