Краткие теоретические сведения. Система n линейных уравнений с n неизвестными x1, x2,
Система n линейных уравнений с n неизвестными x 1, x 2,..., x n
называется системой линейных уравнений n -го порядка; a ij – коэффициенты, b i– свободные члены системы. Численные методы решения систем линейных уравнений делятся на прямые и итерационные [7]. Прямые методы позволяют получить в принципе точное решение за конечное количество арифметических операций, однако при увеличении порядка n системы возрастает погрешность вычисления неизвестных x 1, x 2,..., x n. Итерационные методы позволяют получать решение с заданной точностью на основе алгоритмов, использующих последовательное приближение (итерацию), однако эффективность итерационных алгоритмов существенно зависит от удачного выбора начального приближения и быстроты сходимости итерационного процесса. Один из прямых методов, который достаточно просто реализуется средствами Microsoft Excel, использует вычисление обратной матрицы.
Если представить систему линейных уравнений (1) в матричном виде
где
где Пример Найти решение системы линейных уравнений
двумя методами: прямым, с использованием обратной матрицы, и итерационным. Сравнить полученные решения.
|

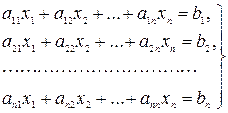 (1)
(1)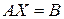 , (2)
, (2) – матрица коэффициентов,
– матрица коэффициентов, – вектор-столбец неизвестных,
– вектор-столбец неизвестных,  – вектор-столбец свободных членов, то решение системы (2) находится следующим образом
– вектор-столбец свободных членов, то решение системы (2) находится следующим образом (3)
(3) – матрица, обратная к матрице
– матрица, обратная к матрице 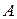 .
.
 (4)
(4)


