ИССЛЕДОВАНИЕ
ДВИЖЕНИЯ ТЕЛ В ДИССИПАТИВНОЙ СРЕДЕ
Таблица 1
| Измеряемая величина
| Номер наблюдения
| | | |
| 1
| 2
| 3
| 4
| 5
| 
| 
| 
|

| 206
| 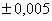
| | |

| 136
| 119
| 90
| 89
| 80
| | 
| |
| t (сек)
| 5,45
| 5,55
| 7,1
| 7,15
| 7,75
| | | 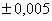
|

| 0,038
| 0,037
| 0,029
| 0,029
| 0,027
| | | |

| 
| | | |

| 
| | | |
Выполнил Чистяков А.О.
Факультет РТ
Группа № 4121
«1» октября 2004
Преподаватель Дедык А.И.
Обработка результатов
1. По полученным данным рассчитываем скорость движения V∞ для каждого шарика.
Формула для расчета скорости движения 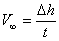 , где
, где
Δh – расстояние между метками,
t – время прохождения шариком расстояния Δh между метками в сосуде.




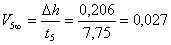
1.1 Рассчитываем диаметр и радиус каждого шарика.
Пусть  – объем шарика, D – диаметр шарика, R – радиус шарика, тогда
– объем шарика, D – диаметр шарика, R – радиус шарика, тогда

 теперь приравниваем
теперь приравниваем  и получаем формулы для расчета диаметра и радиуса шариков
и получаем формулы для расчета диаметра и радиуса шариков  ;
; 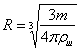









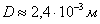
1.2 Вычислим коэффициент вязкости исследуемой жидкости, для каждого из опытов



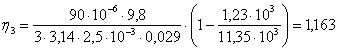

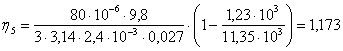
2. Упорядочим  ; проверим на промахи; найдем
; проверим на промахи; найдем  и
и  ;
;
| N
| 1
| 2
| 3
| 4
| 5
| 
| 
| 
|

| 1,095
| 1,162
| 1,163
| 1,173
| 1,175
| | | |

| 119
| 89
| 90
| 80
| 136
| 
| | |
| t (сек)
| 5,55
| 7,15
| 7,1
| 7,75
| 5,45
| | 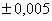
| |

| 206
| | | 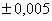
|
R – размах выборки

Up1n=0,64; N=5; P≈95%


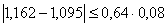

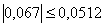
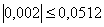
Из этого видно что  промах поэтому
промах поэтому 
исключаем его из таблицы. Теперь таблица
выглядит так:
| N
| 1
| 2
| 3
| 4
| 
| 
| 
|

| 1,162
| 1,163
| 1,173
| 1,175
| | | |

| 89
| 90
| 80
| 136
| 
| | |
| t (сек)
| 7,15
| 7,1
| 7,75
| 5,45
| | 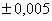
| |

| 2,5
| 2,5
| 2,4
| 2,8
| | | |

| 206
| | | 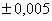
|





2.1 Теперь находим среднее значение

2.2 Находим среднеквадратическое отклонение результатов измерения 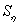

2.3 Найдем средний квадрат отклонения 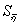

2.4 Высчитаем случайную погрешность результатов измерений
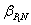 =0,72;
=0,72;  =3,2;N=4; P≈95%
=3,2;N=4; P≈95%
I. 

II. 
2.5 Производим вывод выражений для частных производных от функции

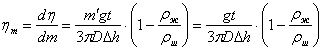





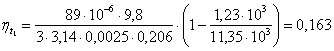
 rdf
rdf




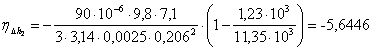


2.6 По каждому набору совместно измеренных значений аргументов и их приборных погрешностей рассчитаем приборную погрешность функции



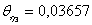

2.7 Вычислить среднюю приборную погрешность функции

2.8 Вычисляем полную погрешность функции

2.9 Запишем результат измерения и округлим его

3. Рассчитайте значения коэффициентов сопротивления r для каждого опыта
Для шара радиуса R коэффициент сопротивления определяется формулой Стокса


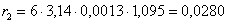

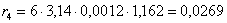

4. Определим время релаксации. Предположим, что скорость прохождения шарика между слоями равна постоянной скорости (скорости равномерного падения шарика), то есть
νi=ν¥;  где
где 






Время релаксации ti очень мало, поэтому шарики до прохождения первой отметки успевают принять постоянную скорость ν¥, т.е. их движение является установившимся на пути от верхней метки к нижней.
5. Определим мощность рассеяния для каждого шарика






6. Графики
См. в конце на миллиметровке
7. Сведем все данные в таблицу

| 113
| 114
| 112
| 120
| 117
| 
| 
|

| 0.5* 
|
| t (сек)
| 5.86
| 5.87
| 5.85
| 5.37
| 5.45
| 
| 
|

| 0.5* 
|

| 200
| |

| 0.5* 
| |
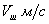
| 0,03413
| 0,03407
| 0,03419
| 0,03724
| 0,03670
| |

| 1,161
| 1,169
| 1,1531
| 1,1092
| 1,1055
|  1,1396 1,1396
|

| 0,003918
| | | | | |

| 
| | | | | |

| 1,162
| 1,163
| 1,173
| 1,175
| 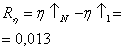
|

| 0,001
| 0,01
| 0,002
| 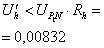
|

| -0,006
| -0,005
| 0,005
| 0,006
| SD 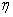 i = 0 i = 0
|
(D 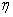 i )2 i )2
| 36∙ 10-6
| 25∙ 10-6
| 25∙ 10-6
| 36∙ 10-6
| S(D fi)2 =122∙ 10-6
|

| 0,03555
| 0,03550
| 0,03657
| 0,03393
| 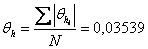
|
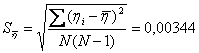 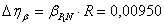      
|
| | | | | | | | | | | | | | |
8. Упорядочим  ; проверим на промахи; найдем
; проверим на промахи; найдем  и
и  ;
;
| N
| 1
| 2
| 3
| 4
| 5
| 
| 
| 
|

| 0,0262
| 0,0269
| 0,0271
| 0,028
| 0,0314
| | | |

| 80
| 89
| 90
| 119
| 136
| 
| | |
| t (сек)
| 7,75
| 7,15
| 7,1
| 5,55
| 5,45
| | 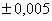
| |

| 206
| | | 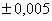
|
R – размах выборки

Up1n=0,64; N=5; P≈95%






 Из этого видно что
Из этого видно что  промах поэтому исключаем его из таблицы. Теперь таблица выглядит так:
промах поэтому исключаем его из таблицы. Теперь таблица выглядит так:
| N
| 1
| 2
| 3
| 4
| 
| 
| 
|

| 0,0262
| 0,0269
| 0,0271
| 0,028
| | | |

| 80
| 89
| 90
| 119
| 
| | |
| t (сек)
| 7,75
| 7,15
| 7,1
| 5,55
| | 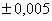
| |

| 206
| | | 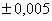
|


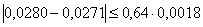


2.1 Теперь находим среднее значение

2.2 Находим среднеквадратическое отклонение результатов измерения 

2.3 Найдем средний квадрат отклонения 

2.4 Высчитаем случайную погрешность результатов измерений
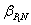 =0,72;
=0,72;  =3,2;N=4; P≈95%
=3,2;N=4; P≈95%
I. 

II. 
2.5 Производим вывод выражений для частных производных от функции





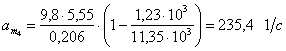






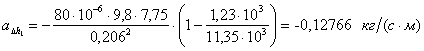
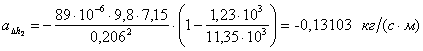
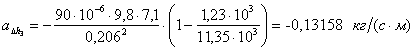

2.6 По каждому набору совместно измеренных значений аргументов и их приборных погрешностей рассчитаем приборную погрешность функции

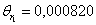
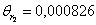


2.7 Вычислить среднюю приборную погрешность функции
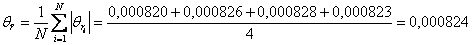
2.8 Вычисляем полную погрешность функции

2.9 Запишем результат измерения и округлим его

Вывод: Коэффициент вязкости ( 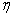 ) полученный и рассчитанный в ходе лабораторных измерений отличается от стандартного значения, в основном из-за погрешностей, допущенных в ходе измерения массы шарика и времени прохождения им между двумя отметками. Для более точного измерения нам необходим электронный секундомер.
) полученный и рассчитанный в ходе лабораторных измерений отличается от стандартного значения, в основном из-за погрешностей, допущенных в ходе измерения массы шарика и времени прохождения им между двумя отметками. Для более точного измерения нам необходим электронный секундомер.
Конрад Гейден История германского фашизма

Государственное социально-экономическое издательство; Москва; 1935





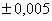







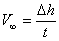 , где
, где



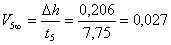
 – объем шарика, D – диаметр шарика, R – радиус шарика, тогда
– объем шарика, D – диаметр шарика, R – радиус шарика, тогда
 теперь приравниваем
теперь приравниваем  и получаем формулы для расчета диаметра и радиуса шариков
и получаем формулы для расчета диаметра и радиуса шариков  ;
; 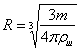









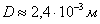



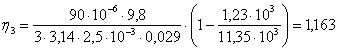

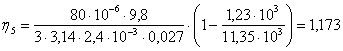
 ; проверим на промахи; найдем
; проверим на промахи; найдем  и
и  ;
;



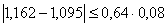

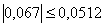
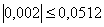
 промах поэтому
промах поэтому 






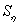

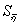

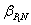 =0,72;
=0,72;  =3,2;N=4; P≈95%
=3,2;N=4; P≈95%



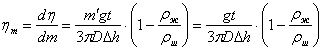





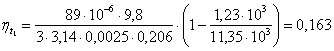
 rdf
rdf



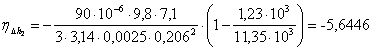





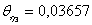






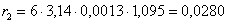

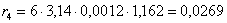

 где
где 

















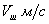

 1,1396
1,1396




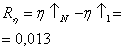

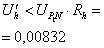

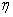 i = 0
i = 0

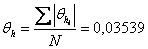
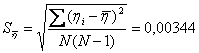
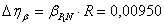





 ; проверим на промахи; найдем
; проверим на промахи; найдем  и
и  ;
;







 Из этого видно что
Из этого видно что  промах поэтому исключаем его из таблицы. Теперь таблица выглядит так:
промах поэтому исключаем его из таблицы. Теперь таблица выглядит так: 

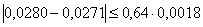














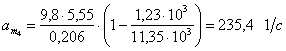






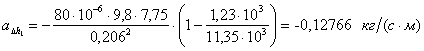
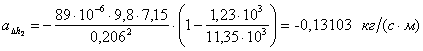
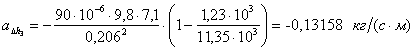


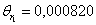
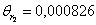


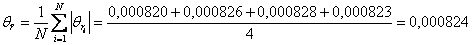


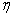 ) полученный и рассчитанный в ходе лабораторных измерений отличается от стандартного значения, в основном из-за погрешностей, допущенных в ходе измерения массы шарика и времени прохождения им между двумя отметками. Для более точного измерения нам необходим электронный секундомер.
) полученный и рассчитанный в ходе лабораторных измерений отличается от стандартного значения, в основном из-за погрешностей, допущенных в ходе измерения массы шарика и времени прохождения им между двумя отметками. Для более точного измерения нам необходим электронный секундомер.



