Частотные характеристики структурных звеньев
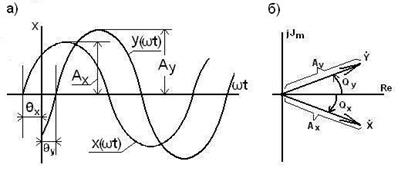
Для определения частотных характеристик рассматривается передача линейным звеном направленного действия гармонического сигнала x( ω t) c амплитудой Аx, угловой частотой ω, начальной фазой θ x: (рис.4,а):
На выходе звена в установившемся режиме гармонический сигнал y( ω t) имеет ту же частоту, но изменившиеся амплитуду Аy и фазу θ y:
Рис. 5
Изменение гармонического сигнала при передаче его звеном характеризуется отношением амплитуд На рис.4,б гармонические сигналы x (ω t) и y( ω t) представлены на в виде векторов
Комплексной частотной передаточной функцией (комплексным коэффициентом передачи) называют отношение вектора выходногогармонического сигнала
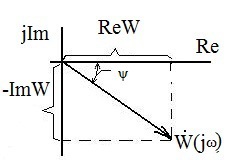
Таким образом комплексная частотная передаточная функция характеризует относительное изменение амплитуды А и фазы ψгармонического сигнала при передаче его звеном или системой. На комплексной плоскости частотную передаточную функцию можно представить неподвижным вектором (рис. 5):
Модуль вектора представляет собой отношение амплитуд:
фаза вектора ψ=θ y -θ x – разность фаз выходного и входного гармонических сигналов. При анализе частотных характеристик более удобной является алгебраическая форма записи комплексной частотной функции с выделением вещественной
Рис.6.
При обратном преобразовании для определения модуля и фазы вектора комплексной частотной функции используют известные соотношения:
Комплексную частотную передаточную функцию при изменении угловой частоты можно представить двумя вещественными характеристиками: амплитудно-частотной А (ω) и фазо-частотной ψ(ω ). Недостатками этих характеристик является сложность их представления в широком диапазоне изменения угловой частоты. Расчет и построение этих характеристик существенно упрощается при использовании логарифмических масштабов. Такие зависимости называют логарифмическими амплитудно-частотными (ЛАЧХ) и фазо-частотными (ЛФЧХ) характеристиками. Логарифмическая амплитудно-частотная характеристика показывает, как изменяется в логарифмическом масштабе в зависимости от угловой частоты амплитуда гармонического сигнала, передаваемого звеном или системой относительно амплитуды входного гармонического сигнала. Для количественного выражения ординат ЛАЧХ использована логарифмическая единица усиления мощности гармонического сигнала 1бел [Б], применяемая в акустике. Она характеризует усиление мощности сигнала в 10 раз. В теории автоматического управления используют понятие усиления амплитуды гармонического сигнала. Мощность гармонического сигнала пропорциональна квадрату его амплитуды, поэтому единице усиления мощности 1 бел соответствует усиление амплитуды сигнала в Логарифмы угловой частоты Аналитическое выражение ЛАЧХ G( ω ) определяется логарифмированием квадрата модуля комплексной частотной функции и умножением на 10 для перевода в дольные единицы усиления мощности, дБ:
График ЛАХЧ строят в логарифмических координатах. Усиление мощности сигнала, в децибелах, откладывают по оси ординат, а логарифмическое увеличение частоты, в декадах, – по оси абсцисс. Расположение характеристики выше оси абсцисс характеризует усиление амплитуды и мощности гармонического сигнала на выходе звена или системы относительно входного. Если характеристика или ее часть расположена ниже оси абсцисс, это соответствует ослаблению амплитуды и мощности сигнала. Логарифмическая фазочастотная характеристика ψ(ω) – это зависимость относительного изменения фазы гармонического сигнала при передаче его звеном или системой от логарифма угловой частоты. На графике изменение фазы ψ, выраженное в угловых градусах или радианах, откладывают по оси ординат. Логарифмическую частоту, в декадах, откладывают по оси абсцисс. Логарифмические амплитудно- и фазо- частотные характеристики обычно совмещают по координате частоты, или располагают одну под другой. Свойства логарифмических частотных характеристик (ЛЧХ): - форма ЛЧХ и не зависит от параметров звена - коэффициента усиления и постоянной времени; она определяется формулой частотной передаточной функции; - ЛАЧХ и ЛФЧХ смещаются по оси абсцисс влево при увеличении постоянной времени звена, вправо - при уменьшении постоянной времени; - ЛАЧХ смещается по оси ординат вверх при увеличении коэффициента усиления, вниз - при уменьшении коэффициента усиления; положение ЛФЧХ в координатных осях не зависит от коэффициента усиления звена. Для определения комплексной частотной передаточной функции и амплитудно-фазовой характеристик апериодического звена 1-го порядка гармонические сигналы входной х( ω t) и выходной у( ω t) в уравнении (1) представлены в комплексной форме:
Комплексная частотная передаточная функция в соответствии с выражением (17) имеет следующий вид:
Сопоставление полученного выражения с формулой (7) операторной передаточной функции апериодического звена 1-го порядка показывает их полную идентичность. Поэтому комплексную частотную функцию звена или системы автоматического управления можно выразить из операторной передаточной функции, заменив в ней множитель «р» на «j ω ». Для определения амплитудно-частотной и фазочастотной характеристик, надо представить комплексную частотную передаточную функцию (20) в алгебраической форме в виде суммы вещественной и мнимой частей:
Используя выражение (17) и (18) можно получить формулы, определяющие зависимости изменения модуля
Логарифмическая амплитудно-частотная характеристика апериодического звена 1-го порядка определяются в соответствии с выражением (19) логарифмированием модуля частотной передаточной функции (20):
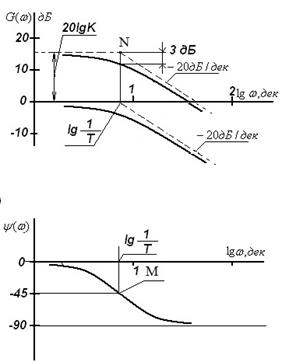
График ЛАЧХ апериодического звена 1-го порядка показан на рис.6,а. В инженерных расчетах обычно используют упрощенные ЛАЧХ, составленные из линейных отрезков, что позволяет избежать громоздких вычислений. Горизонтальный отрезок располагают на уровне
Наклонный отрезок с крутизной наклона «минус» 20дБ/дек сопрягается с горизонтальным отрезком характеристики в точке N при логарифмической частоте а) б)
Рис.7 Наибольшая погрешность линеаризации ЛАЧХ апериодического звена 1-го порядка имеет место при логарифмической частоте сопряжения отрезков Правило: для построения линеаризованной ЛАЧХ апериодического звена 1-го порядка надо вычислить логарифмические координаты точки N сопряжения горизонтального и наклонного отрезков характеристики [ Коэффициент усиления K исследуемых апериодических звеньев 1-го порядка равен 1, поэтому горизонтальный отрезок линеаризованной характеристики расположен на оси абсцисс. График логарифмической фазо-частотной характеристики апериодического звена 1-го порядка описывается функцией арктангенса (22), и изменяется в пределах от 0 до -90 град. При частоте Комплексная частотная передаточная функция колебательного звена 2-го порядка получена из уравнения в комплексной форме с гармоническими переменными
В соответствии с выражением (5) она имеет следующий вид:
Для определения амплитудночастотной и фазочастотной характеристик, надо представить комплексную частотную передаточную функцию (24) в виде суммы вещественной и мнимой частей:
Используя выражение (17) и (18) получены формулы, определяющие зависимости изменения модуля
Логарифмическая амплитудно-частотная характеристика колебательного звена 2-го порядка определяются в соответствии с выражением (19) логарифмированием модуля частотной передаточной функции (25):
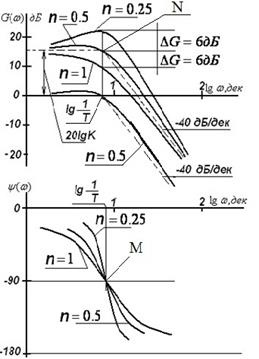
Графики ЛАЧХ колебательного звена 2-го порядка для коэффициентов затухания n =1; 0,5; 0,25 показаны на рис.7,б. Упрощенная ЛАЧХ, составленная из линейных отрезков, выделена для n =0,5 штриховыми линиями. Горизонтальный отрезок расположен по оси абсцисс на уровне
Коэффициент усиления K исследуемого колебательного звена 2-го порядка равен 1, поэтому горизонтальный отрезок линеаризованной характеристики расположен на оси абсцисс. Характеристики исследуемого звена выделены на рис. 7,а штриховыми линиями.
ЛФЧХ колебательного звена 2-го порядка описывается функцией арктангенса (27) и изменяется в пределах от 0 до -180 град. При частоте
|

 .
.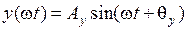 .
.
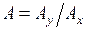 и разностью фаз ψ=θу-θх.
и разностью фаз ψ=θу-θх. ,
, 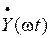 , вращающихся с угловой частотой ω. Модуль каждого вектора
, вращающихся с угловой частотой ω. Модуль каждого вектора  равен амплитуде соответствующего сигнала, а их положение на комплексной плоскости определяется начальными фазами. Векторы этих сигналов в комплексной форме имеют следующее выражение:
равен амплитуде соответствующего сигнала, а их положение на комплексной плоскости определяется начальными фазами. Векторы этих сигналов в комплексной форме имеют следующее выражение: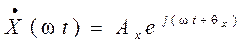 ,
,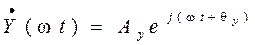 .
. 
 к вектору входного сигнала
к вектору входного сигнала 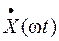 :
: . (17)
. (17)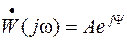 .
.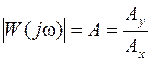 ,
,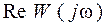 и мнимой
и мнимой 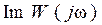 частей:
частей: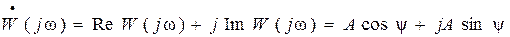 .
.
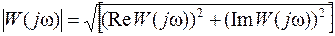 ; (17)
; (17)
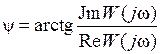 . (18)
. (18)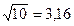 раза. Практически используют дольную единицу - децибел (1[дБ]=0,1Б), соответствующую усилению мощности сигнала в
раза. Практически используют дольную единицу - децибел (1[дБ]=0,1Б), соответствующую усилению мощности сигнала в 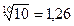 раза и увеличению амплитуды в
раза и увеличению амплитуды в 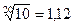 раза.
раза.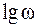 выражаются в декадах; 1 дек соответствует увеличению частоты в 10 раз.
выражаются в декадах; 1 дек соответствует увеличению частоты в 10 раз.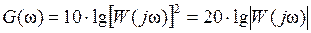 . (19)
. (19)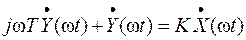 .
.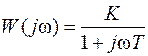 . (20)
. (20)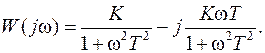
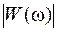 и фазы ψ(ω) вектора частотной функции от угловой частотыω:
и фазы ψ(ω) вектора частотной функции от угловой частотыω: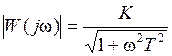 , (21)
, (21) . (22)
. (22)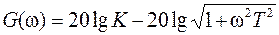 . (23)
. (23)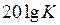 . Аналитическое выражение для наклонного отрезка может быть получено из второго слагаемого формулы (23), если пренебречь единицей под знаком радикала:
. Аналитическое выражение для наклонного отрезка может быть получено из второго слагаемого формулы (23), если пренебречь единицей под знаком радикала: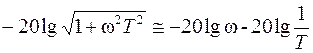 .
. .
.
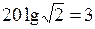 дБ. График линеаризованной ЛАЧХ выделен на рис.7,а штриховыми линиями.
дБ. График линеаризованной ЛАЧХ выделен на рис.7,а штриховыми линиями. ;
; 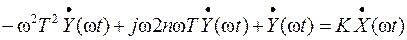 .
.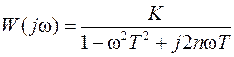 . (24)
. (24)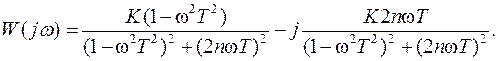
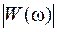 (АЧХ) и фазы ψ(ω) (ФЧХ) вектора частотной функции от угловой частотыω:
(АЧХ) и фазы ψ(ω) (ФЧХ) вектора частотной функции от угловой частотыω: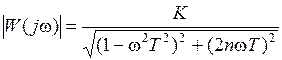 , (25)
, (25)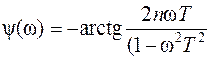 . (26)
. (26)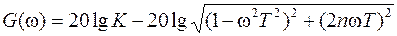 . (28)
. (28)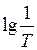 с наклоном «минус» 40 дБ/дек. Наибольшая погрешность линеаризации ЛАЧХ при логарифмической частоте сопряжения отрезков
с наклоном «минус» 40 дБ/дек. Наибольшая погрешность линеаризации ЛАЧХ при логарифмической частоте сопряжения отрезков 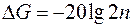 . (28)
. (28)


