Динамические характеристики структурных звеньев
Переходной функцией
Рис.1 График переходной функции наглядно, с физической точки зрения, показывает, какие изменения претерпевает входной ступенчато изменяющийся сигнал при прохождении через динамическое звено. Операторным коэффициентом передачи
Операторная передаточная функция динамического звена представляет собой аналитическое выражение переходной функции в операторной форме: Переходная функция апериодического звена 1-го порядка может быть получена из решения дифференциального уравнения (1) c входной переменной в виде единичной функции Переходная функция апериодического звена 1-го порядка в имеет следующий вид:
График переходной функции показан на рис.1,б. Он представляет собой экспоненциальную зависимость нарастания выходной переменной при ступенчатом изменении входной. Наибольшая скорость нарастания выходного сигнала имеет место в начале процесса и определяется отношением Операторная передаточная функция апериодического звена 1-го порядка определяется из уравнения (1) звена в операторной форме:
В соответствии с выражением (5) она имеет следующий вид:
Свойствами апериодического звена 1-го порядка обладают электрические цепи, составленные из конденсатора и резистора или индуктивной катушки и резистора (рис.2,а, б). Переходные процессы, протекающие в электрической R-C цепи при подаче на вход напряжения коммутатора K, характеризуются следующим дифференциальным уравнением:
Полученное дифференциальное уравнение соответствует уравнению (1) апериодического звена 1-го порядка. Из сопоставления коэффициентов при переменных в уравнениях следует, что коэффициент усиления цепи K =1, а постоянная времени определяется формулой: T=RC. (8) .
Рис.2 Передача сигнала в электрической цепи, составленной из индуктивной катушки и резистора характеризуется дифференциальным уравнением:
Выходным сигналом такой цепи является падение напряжения на сопротивлении резистора R. Коэффициент усиления цепи с индуктивной катушкой K =1, постоянная времени определяется формулой:
Переходная функция колебательного звена второго порядка, полученная из решения дифференциального уравнения (2) звена при входном сигнале в виде единичной функции, имеет вид:
Здесь Графики переходной функции колебательного звена для коэффициентов относительного затухания: n =0,2; 0,5; 1 показаны на рис.3.
Рис.3 Из рисунка видно, что колебательность переходной функции зависит от коэффициента затухания. При n =0,5 колебательный характер переходной функции близок к апериодическому, а при n =1 переходная функция становится монотонной. Уравнение колебательного звена 2-го порядка в операторной форме получено из дифференциального уравнения (2) звена:
Отсюда операторная передаточная функция колебательного звена 2-го порядка имеет следующий вид:
Свойствами колебательного звена 2-го порядка обладает электрическая цепь составленная из конденсатора емкостью С, катушки с индуктивностью L и резистора с сопротивлением R (рис.4).
Рис.4. Схема колебательного звена 2-го порядка
Уравнение равновесия напряжений для этой цепи имеетследующий вид:
Ток, протекающий по конденсатору, связан с напряжением конденсатора соотношением:
Из сопоставления уравнений (2) и (12) параметры колебательного звена определяется следующими формулами: постоянная времени - частота свободных колебаний - коэффициент относительного затухания - коэффициент усиления - К =1.
|

 звена направленного действия называют изменение во времени выходного сигнала звена при ступенчатом изменении входной переменной в виде единичной функции 1(t) (рис.1):
звена направленного действия называют изменение во времени выходного сигнала звена при ступенчатом изменении входной переменной в виде единичной функции 1(t) (рис.1):


 илиоператорной передаточной функцией называют отношение операторного изображения выходного сигнала
илиоператорной передаточной функцией называют отношение операторного изображения выходного сигнала  к операторному изображению входного сигнала
к операторному изображению входного сигнала  при нулевых начальных условиях:
при нулевых начальных условиях: . (5)
. (5)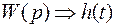 .
. :
: . (6)
. (6) . Длительность изменения выходной переменной апериодического звена до установившегося уровня считают равной t =3 Т. При этом выходная переменная достигает установившегося уровня на 95%.
. Длительность изменения выходной переменной апериодического звена до установившегося уровня считают равной t =3 Т. При этом выходная переменная достигает установившегося уровня на 95%. .
. . (7)
. (7)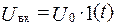 в результате замыкания
в результате замыкания .
.
 или:
или:  .
. , (9)
, (9) . (10)
. (10)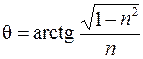 - начальная фаза гармонической функции.
- начальная фаза гармонической функции.
 .
. . (11)
. (11)
 .
. . После подстановки этого выражения в уравнение цепи получено уравнение, идентичное каноническому уравнению (2) колебательного звена 2-го порядка.
. После подстановки этого выражения в уравнение цепи получено уравнение, идентичное каноническому уравнению (2) колебательного звена 2-го порядка. . (12)
. (12) , (13)
, (13)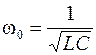 , (14)
, (14) , (15)
, (15)


