Построение развертки призмы методом нормального сечения
На примере, рассмотренном в приложении 1, для построения 1. Пересекаем боковые грани призмы плоскостью, перпендикулярной к ребрам. 2. Строим проекции сечения и находим натуральную величину фигуры сечения. 3. На прямой откладываем отрезки, равные сторонам фигуры сечения. 4. Через полученные точки проводим прямые, перпендикулярные этой прямой, и откладываем на них отрезки, равные натуральной величине боковых ребер призмы. Полученные точки соединяем отрезками прямых. В рассмотренном нами случае секущая плоскость α, заданная на чертеже пересечением горизонтали и фронтали, перпендикулярна боковым ребрам призмы α┴[AA']; [BB']; [CC']. Следовательно, полученное сечение – треугольник 123 – является нормальным (от слова «нормаль» - перпендикуляр) сечением призмы. Преобразованная проекция На прямой откладываем отрезки [12], [23], [31], равные сторонам фигуры сечения Через точки 1,2,3 проводим перпендикуляры и откладываем по разные стороны от прямой 1-1 отрезки, равные натуральной величине ребер призмы. Размеры ребер берем с проекции на плоскости π4, где они проецируется без искажения: [A1] = [A4 14]; [B2] = [B4 24]; [C3] = [C4 34]. К полученной развертке боковой поверхности усеченной призмы достраиваем нижнее основание – треугольник АBС и натуральную величину сечения – треугольник 123. Полученная плоская фигура есть полная развертка усеченной части призмы.
|

 есть натуральная величина этого нормального сечения.
есть натуральная величина этого нормального сечения.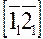 ;
; 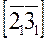 ;
;  .
.


