Промышленные способы подвода и отвода теплоты
Промышленные способы подвода и отвода теплоты (теплообмен в химико-технологических аппаратах) 3.2.1. Теплообмен в текучих средах
Проведение реакций между двумя или более реагентами, находящимися в жидком или газообразном состоянии, представляет собой один из наиболее распространенных процессов химической технологии. На полноту химического превращения в реальном реакционном аппарате (реакторе) влияют многие факторы: характер основной химической реакции, то есть зависимость скорости реакции от концентрации реагентов; тепловой эффект реакции; установившаяся в зоне реагирования температура; наличие побочных реакций; подвод (или отвод) теплоты от реакционной массы; количество подаваемых в зону реакции реагирующих веществ и время их пребывания в зоне реакции; характер гидродинамического перемешивания реакционной массы и т.д. Для полного анализа химических, физико-химических и физических процессов в гомогенном жидкофазном реакторе, когда химическая реакция не сопровождается образованием паровой или твердой фаз, необходимо иметь: 1) стехиометрическое уравнение реакции и константу ее равновесия; 2) уравнения неразрывности всех компонентов с учетом источника (стока) массы за счет химической реакции; 3) уравнение гидродинамики потоков с учетом возможного изменения объемов продуктов реакции; 4) уравнение переноса энергии с учетом источника (стока) теплоты за счет теплоты реакции; 5) уравнение переноса реагирующих компонентов за счет конвективного и диффузионного механизмов, также с учетом стока (источника) массы; 6) кинетическое уравнение химической реакции, определяющее зависимость скорости химического превращения от концентрации реагентов; 7) зависимость константы скорости реакции от температуры и энергии активации (уравнение Аррениуса). Такая система алгебраических и дифференциальных уравнений с соответствующими начальными и граничными условиями полностью определяет поля температуры, концентраций и скоростей движения реагентов в реакционном аппарате. Усреднение этих полей на выходе из аппарата позволяет получить интегральную степень превращения, достигаемую при заданных условиях работы. Однако решение общей системы уравнений, описывающей протекающий в реакторе процесс, не представляется возможным ввиду значительной сложности нелинейных дифференциальных уравнений переноса с коэффициентами (вязкость, коэффициенты теплопроводности, диффузии и т.д.), зависящими от искомого распределения температуры. Как известно, при анализе сложных процессов, нужны приемлемые упрощения их описания. В теории химических реакторов принято полагать, что вместо сложного химического, теплового и диффузионного взаимодействия можно анализировать более простые предельные варианты процессов: 1) скорость собственно химической реакции значительно меньше скорости подачи реагентов в аппарат и транспортировки их из основной массы потока в зону непосредственно реагирования, при этом интегральная скорость всего процесса не зависит от интенсивности массообменных процессов, а определяется кинетикой химической реакции (концентрацией и температурой реагентов) – это так называемая кинетическая область протекания процесса; 2) скорость химической реакции велика, и общий темп химического превращения определяется скоростью транспортировки реагентов в зону реагирования – диффузная область; 3) скорость реакции зависит в сравнимой степени как от диффузионных процессов, так и от кинетики химической реакции – смешанная область. В некоторых простых случаях быстрого протекания химических и диффузионных процессов общую степень превращения может лимитировать скорость подвода реагентов в реактор (балансовая задача). Уравнение скорости химической реакции (быстроты изменения концентраций реагентов со временем) записывается в степенной форме относительно концентрации реагентов:
где a1 и a2 – порядки реакции по компонентам 1 и 2, получаемые, как правило, опытным путем; k – константа скорости реакции. Общепринятой является запись температурной зависимости k в виде уравнения Аррениуса
где Е – энергия активации данной реакции; R – газовая постоянная; k o – предэкспоненциальный множитель, зависящий от вероятности реагирования молекул реагентов при их столкновении. Значение k o определяется опытным путем для конкретных реакций, проводимых при разных температурах Т (в К). При анализе температурных режимов работы реакционных аппаратов принято рассматривать следующие предельные и промежуточные варианты: 1) изотермический режим, при котором постоянство температуры во всем реакционном объеме аппарата поддерживается за счет достаточно интенсивного теплообмена с окружающей средой, позволяющего подводить к реакционной массе (или отводить от нее) всю поглощаемую (или выделяемую) теплоту химической реакции; кроме того, должно быть обеспечено полное перемешивание реагирующей массы, чтобы не было температурных градиентов; 2) адиабатический режим предполагает отсутствие теплообмена между зоной реакции и окружающей средой, при этом выделяющаяся за счет реакции теплота идет на разогрев при экзотермических реакциях, а при эндотермических реакциях происходит охлаждение реакционной массы. В проточных реакторах вытеснения температура увеличивается или падает по длине адиабатического реактора; 3) реальный промежуточный режим соответствует частичному отводу теплоты реакции. При этом за счет изменения интенсивности теплоотвода оказывается возможным регулировать температуру реакционной массы во времени для периодических процессов либо по длине проточного аппарата непрерывного действия; 4) при автотермическом режиме теплота реакции используется для поддержания ее температурного режима. Практически это означает подогрев исходных реагентов продуктами реакции, разогретыми в результате экзотермического процесса. Из уравнений химической кинетики следует, что температура оказывает наиболее значительное влияние на скорость химической реакции в кинетической области процесса.
Для экзотермической обратимой реакции определить оптимальную температуру, при которой скорость будет максимальной, можно, если, записав уравнение скорости обратимой реакции, приравнять к нулю производную ¶r/¶ T = 0.
|

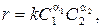 (3.54)
(3.54)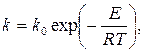 (3.55)
(3.55)
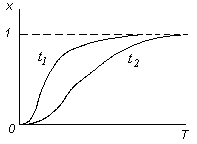 Зависимость степени превращения от температуры для необратимых реакций при некоторых временах процесса реагирования t1 > t2 представлена на рис. 3.13. При фиксированном времени реагирования в случае низкой температуры степень превращения мала. Затем она значительно увеличивается с возрастанием Т, асимптотически приближаясь к полной степени превращения (х = 1). По мере увеличения времени, предоставленного для проведения реакции, можно либо увеличить степень превращения при сохранении температуры реакции, либо уменьшить Т при сохранении необходимой конечной степени превращения. Для проточного реактора увеличение времени реагирования может быть достигнуто увеличением объема реактора или снижением его производительности.
Зависимость степени превращения от температуры для необратимых реакций при некоторых временах процесса реагирования t1 > t2 представлена на рис. 3.13. При фиксированном времени реагирования в случае низкой температуры степень превращения мала. Затем она значительно увеличивается с возрастанием Т, асимптотически приближаясь к полной степени превращения (х = 1). По мере увеличения времени, предоставленного для проведения реакции, можно либо увеличить степень превращения при сохранении температуры реакции, либо уменьшить Т при сохранении необходимой конечной степени превращения. Для проточного реактора увеличение времени реагирования может быть достигнуто увеличением объема реактора или снижением его производительности.
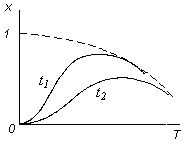 Для обратимых реакций влияние температуры на степень превращения также имеет S-образный характер, но верхний предел кривых соответствует не полной степени превращения, а равновесным концентрациям, зависящим, в свою очередь, от температуры реакции. Кривая равновесия представлена огибающей пунктирной линией (рис. 3.14).
Для обратимых реакций влияние температуры на степень превращения также имеет S-образный характер, но верхний предел кривых соответствует не полной степени превращения, а равновесным концентрациям, зависящим, в свою очередь, от температуры реакции. Кривая равновесия представлена огибающей пунктирной линией (рис. 3.14).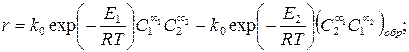 (3.56)
(3.56)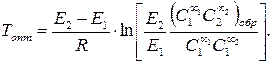 (3.57)
(3.57)


