Сұйық - бу- жүйедегі тепе-теңдік. Рауль заңы

Идеал қоспалар Рауль және Дальтон заңдарына бағынады. Рауль заңы бойынша: әр құрастырушының парциалдық кысымы (р_A немесе р_В) олардың сұйық қоспадағы мольдік үлестеріне тура пропорционал болады:

 

р_А = Р_А∙х_А р_В = Р_В ∙ х_В = Р_В ∙(1-х_А) (1)

 

мұнда р_А, р_В - төмен температурада қайнайтын және жоғары температурада қайнайтын құрастырушылардың парциалдық қысымы;

Р_А, Р_В - берілген температурадағы таза құрастырушылар А мен В –ның қаныққан буларының қысымы;

х_А және 1- х_А - А мен В құрастырушылардың сұйық қоспадағы мольдік үлестері.

Сонымен бірге, Дальтон заңы бойынша құрастырушылардың парциалдық қысымдары:

р_А = Р∙у_А р_В = Р·(1- у_А) (2)

 

мұнда Р - жүйедегі жалпы қысым;

у_А және (1- у_А) - А мен В құрастырушылардың булы қоспадағы мольдік үлестері.

р_А·х_А=Р·у_А; р_В·(1-х_А) =Р·(1- у_А) (3)

 

Бұл теңдеуден төмен температурада қайнайтын құрастырушының булы қоспадағы мольдік үлесін:

у_А= (р_А/Р) ·х_А немесе (1- у_А) = (р_В/Р)·(1-х_А) (4)

анықтауға болады.

 

Әдетте ректификация процесі тұрақты қысымда өткізіледі, яғни р =соnst. Сондықтан, идеал бинарлы қоспалардың тепе-тендігі р =соnst жағдайда қарастырылады. (4) – тендеудің х_А бойынша шешуін тапсақ:

х_А=(Р- р_В)/(р_А- р_В) (5)

 

ТҚ-ның қайнау температурасы t_ТҚ және ЖҚ-ның t_ЖҚ аралығындағы р_А және р_В–лар дың белгілі мәндерімен (5) - теңдеуден х мәнін, ал (4) - теңдеуден у мәнін анықтауға болады.

 

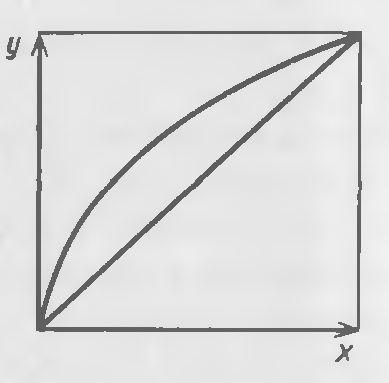
Фазалар ережесінен ректификация процесі үшін еркіндік дәреже С=2-ге тең. Демек, тепе-тендік байланысын екі айнымалы шамалар арқылы өрнектеуге болады: р және х; t және х; р және t; х және у. Егер р =соnst болса, тепе-тендік байланысын t = f(x,y) немесе у = f(x) координаталарында өрнектеуге болады.

Ректификация процесін талдау үшін t-x,y диаграммасының негізінде салынған у-х диаграмма қолайлы (сур.1).

 

Сурет 1. Тепе-тендік диаграммасы

Тепе-тендік у*= f(x) сызығы төмендегі теңдеумен өрнектеледі:

у*_А = (Р_А/Р) ·х_А немесе у*_А= Р_Ах_А/ (Р_А х_А+ Р_В(1- х_А)) (6)