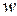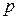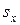Выборочное наблюдение
Задача 16. Используя данные о молочной продуктивности коров кг/день была сформирована 5% выборка из 150 коров человек.
Таблица 54
| Показатель
| Вариант 1
| Вариант 2
| Вариант 3
| Вариант 4
| Вариант 5
| | Надой, кг/день
| 13,98
| 13,92
| 14,42
| 13,76
| 14,16
| 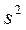
| 0,98617
| 1,05396
| 0,58081
| 1,13664
| 0,99436
| |
| Вариант 6
| Вариант 7
| Вариант 8
| Вариант 9
| Вариант 10
| | Надой, кг/день
| 14,1
| 14,06
| 13,98
| 14,12
| 14,06
| 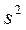
| 0,82886
| 1,03664
| 0,97275
| 0,71034
| 0,99638
| |
| Вариант 11
| Вариант 12
| Вариант 13
| Вариант 14
| Вариант 15
| | Надой, кг/день
| 14,28
| 13,92
| 14,24
| 13,72
| 14,18
| 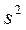
| 0,61906
| 1,04054
| 0,78765
| 1,20966
| 0,90027
| Необходимо определить
1. Для случайного бесповторного отбора:
· среднюю и предельную (с вероятностью 0,954 (при 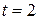 )) ошибку выборки; )) ошибку выборки;
· на сколько необходимо изменить численность выборки, чтобы средняя, предельная ошибка изменилась до (табл. 55):
Таблица 55
| Вариант 1
| Вариант 2
| Вариант 3
| Вариант 4
| Вариант 5
| | ±0,1
| ±0,06
| ±0,15
| ±0,9
| ±0,11
| | Вариант 6
| Вариант 7
| Вариант 8
| Вариант 9
| Вариант 10
| | ±0,2
| ±0,07
| ±0,3
| ±0,19
| ±0,13
| | Вариант 11
| Вариант 12
| Вариант 13
| Вариант 14
| Вариант 15
| | ±0,65
| ±0,2
| ±0,04
| ±0,01
| ±0,03
| 2. Повторить расчеты для случайного повторного отбора.
Задача 17. Методом бесповторного отбора из общей численности молочного стада была проведена 5% выборка.
Таблица 56
| № варианта
| Численность выборки

| Доля коров старше 5лет в выборке
| Уровень доверительной вероятности
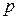
| № варианта
| Численность выборки

| Доля коров старше 5лет в выборке
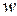
| Уровень доверительной вероятности
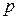
| |
|
| 0,3
| 0,7287
|
|
| 0,3
| 0,9426
| |
|
| 0,2
| 0,7699
|
|
| 0,3
| 0,9545
| |
|
| 0,3
| 0,8064
|
|
| 0,2
| 0,9643
| |
|
| 0,3
| 0,8385
|
|
| 0,3
| 0,9836
| |
|
| 0,2
| 0,9426
|
|
| 0,2
| 0,9876
| |
|
| 0,3
| 0,9545
|
|
| 0,2
| 0,9907
| |
|
| 0,3
| 0,9643
|
|
| 0,3
| 0,9109
| |
|
| 0,1
| 0,9836
|
|
| 0,3
| 0,9281
| |
|
| 0,2
| 0,9876
|
|
| 0,2
| 0,9426
| |
|
| 0,3
| 0,9907
|
|
| 0,3
| 0,9545
| Определить с заданной вероятностью 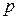 пределы, в которых находится доля коров старше 5лет. Повторить расчет для повторного отбора. пределы, в которых находится доля коров старше 5лет. Повторить расчет для повторного отбора.
Задача 18. По району имеются данные об общей численности молочного стада КРС.
Таблица 57
| № варианта
| Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
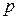
| Стандартная ошибка
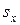
| № варианта
| Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
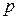
| Стандартная ошибка
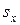
| |
|
| 0,7287
| 1,1
|
|
| 0,9426
| 1,3
| |
|
| 0,7699
| 1,2
|
|
| 0,9545
| 1,2
| |
|
| 0,8064
| 1,2
|
|
| 0,9643
| 1,3
| |
|
| 0,8385
| 1,1
|
|
| 0,9836
| 1,3
| |
|
| 0,9426
| 1,3
|
|
| 0,9876
| 1,2
| |
|
| 0,9545
| 1,2
|
|
| 0,9907
| 1,1
| |
|
| 0,9643
| 1,3
|
|
| 0,9109
| 1,1
| |
|
| 0,9836
| 1,3
|
|
| 0,9281
| 1,2
| |
|
| 0,9876
| 1,2
|
|
| 0,9426
| 1,2
| |
|
| 0,9907
| 1,1
|
|
| 0,9545
| 1,1
| Необходимо определить численность выборки с заданной вероятностью 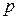 , предельная ошибка среднего надоя не должна превышать 0,2 кг. , предельная ошибка среднего надоя не должна превышать 0,2 кг.
Задача 19. По области изучается доля хозяйств урожайность, в которых превышает 22ц/га. Известно, что:
Таблица 58
| № варианта
| Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
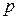
| Доля хозяйств с урожайностью более 22ц/га.
| № варианта
| Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
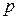
| Доля хозяйств с урожайностью более 22ц/га.
| |
|
| 0,7287
| 0,5
|
|
| 0,9426
| 0,4
| |
|
| 0,7699
| 0,6
|
|
| 0,9545
| 0,3
| |
|
| 0,8064
| 0,7
|
|
| 0,9643
| 0,6
| |
|
| 0,8385
| 0,8
|
|
| 0,9836
| 0,8
| |
|
| 0,9426
| 0,4
|
|
| 0,9876
| 0,4
| |
|
| 0,9545
| 0,6
|
|
| 0,9907
| 0,6
| |
|
| 0,9643
| 0,5
|
|
| 0,9109
| 0,5
| |
|
| 0,9836
| 0,4
|
|
| 0,9281
| 0,7
| |
|
| 0,9876
| 0,8
|
|
| 0,9426
| 0,4
| |
|
| 0,9907
| 0,4
|
|
| 0,9545
| 0,5
| Необходимо определить необходимую численность выборки для бесповторного и повторного отборов.

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Разработка товарной и ценовой стратегии фирмы на российском рынке хлебопродуктов В начале 1994 г. английская фирма МОНО совместно с бельгийской ПЮРАТОС приняла решение о начале совместного проекта на российском рынке. Эти фирмы ведут деятельность в сопредельных сферах производства хлебопродуктов.
МОНО – крупнейший в Великобритании...
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Сила, с которой тело притягивается к Земле, называется силой тяжести...
СПИД: морально-этические проблемы Среди тысяч заболеваний совершенно особое, даже исключительное, место занимает ВИЧ-инфекция...
|
Ведение учета результатов боевой подготовки в роте и во взводе Содержание журнала учета боевой подготовки во взводе. Учет результатов боевой подготовки - есть отражение количественных и качественных показателей выполнения планов подготовки соединений...
Сравнительно-исторический метод в языкознании сравнительно-исторический метод в языкознании является одним из основных и представляет собой совокупность приёмов...
Концептуальные модели труда учителя В отечественной литературе существует несколько подходов к пониманию профессиональной деятельности учителя, которые, дополняя друг друга, расширяют психологическое представление об эффективности профессионального труда учителя...
|
|

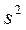
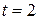 )) ошибку выборки;
)) ошибку выборки;