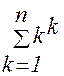Задание на лабораторную работу. 1. Написать функцию, использующую метод Ньютона для вычисления квадратного корня
1. Написать функцию, использующую метод Ньютона для вычисления квадратного корня. Метод Ньютона вычисления квадратного корня из числа x начинается с выбора начального приближения y. Это приближение считается достаточно точным, если | x - y2 | <= err, где err – некоторая заранее определенная погрешность. В противном случае более точным приближением будет 1/2 *(y + x/y), которое можно вычислить и точно так же подвергнуть проверке на погрешность. Для получения абсолютной величины числа используйте функция abs: abs(-5) = 5. Пример: % вычисления квадратного корня из числа 5 % начальное приближение 1 % уровень допустимой погрешности 0.05 ?- newton(5, 1, 0.05, Z) Z=2.2380953 2. Написать рекурсивную и итерационную программы возведения числа в степень. Предполагается использование только натуральных чисел. Возведение в степень представить как повторяющееся умножение. 3. Написать функции для вычисления N-го числа последовательности Фибоначчи. Каждое следующее число последовательности Фибоначчи вычисляется как сумма двух предыдущих. Два первых числа равны единице. Контрольные вопросы 1. Треугольное число с индексом N – это сумма всех натуральных чисел до N включительно. Напишите рекурсивную и итерационную программы, задающую отношение triangle(N, T), истинное, если T – треугольное число с индексом N. 2. Написать рекурсивную и итерационную программы, реализующую вычисления, заданные формулой: 3. Определить процедуру between(N1, N2, X), которая порождает все целые числа X, отвечающие условию N1 £ X £ N2. 4. Написать процедуру, результатом которой будет выражение, являющееся факториалом числа, и в котором числа (сомножители) упорядочены в порядке возрастания. Например, ?- fact(3, S) S=1*2*3 Лабораторная работа №3 Рекурсивные структуры данных
|