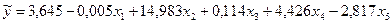Порядок выполнения работы в системе Excel

Лабораторная работа № 3

 

Классическая модель линейной регрессии

 

Задания:

 

1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов по данным в соответствии с вариантом.

2. Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.

3. Оцените с помощью F-критерия Фишера-Снедекора значимость уравнения линейной регрессии и показателя тесноты связи. Определите множественный коэффициент корреляции и детерминации и скорректированный коэффициент детерминации.

4. Оцените статистическую значимость коэффициентов регрессии с помощью t- критерия Стьюдента.

5. Оцените качество уравнения через среднюю ошибку аппроксимации.

6. Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы.

7. Постройте модель в естественной форме только с информативными факторами и оцените ее параметры.

8. Постройте модель в стандартизованном масштабе и проинтерпретируйте ее параметры.

9. Рассчитайте прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений.

10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости .

11. По полученным результатам сделайте экономический вывод.

 

 

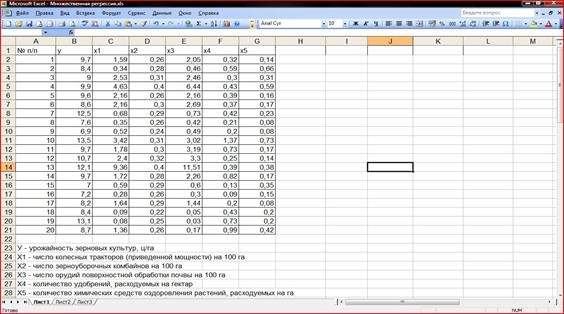
Порядок выполнения работы в системе Excel

Запустить диалоговую систему Excel. Ввести данные для проведения регрессионного анализа. Окно с исходными данными представлено на рисунке 1.

 

Рисунок 1. Таблица с исходными данными.

 

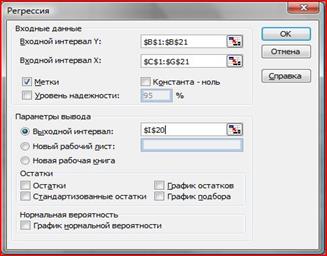
Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов по данным в соответствии с вариантом.

Для построения линейного уравнения множественной регрессии воспользуемся инструментом анализа данных Регрессия. Порядок действий следующий:

а) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;

б) заполните диалоговое окно ввода данных и параметров ввода (рис. 2). При заполнении параметра входной интервал Х в диалоговом столбце следует указать все столбцы, содержащие значения факторных признаков.

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал Х – диапазон, содержащий данные факторов независимого признака;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист - можно задать произвольное имя нового листа.

Рисунок 2 – Диалоговое окно ввода параметров инструмента Регрессия

 

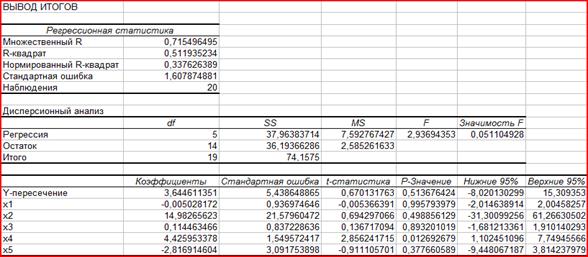
Результаты регрессионного анализа представлены на рисунке 3.

Рисунок 3 – Результат применения инструмента Регрессия

 

По результатам вычислений составим уравнение множественной регрессии:

Величина b₀ не интерпретируется.

Коэффициенты регрессии показывают среднее изменение результативного признака с изменением на 1 единицу своего измерения данного фактора при условии постоянства всех остальных.

Коэффициент чистой регрессии b₁ = -0,005 указывает, что с увеличением числа колесных тракторов на единицу на 100 га, урожайность снижается на 0,005 ц/га, при фиксированном значении остальных факторов. Для остальных коэффициентов делаются аналогичные выводы. Сравнивать коэффициенты чистой регрессии не следует, так как они зависят от единиц измерения каждого признака и потому не сопоставимы между собой.

Следует отметить, что отрицательные знаки коэффициентов регрессии в нашем примере противоречат экономической теории связи между признаками.