Особенности практического применения регрессионных моделей
Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т. е., решение задачи возможно лишь тогда, когда столбцы матрицы исходных данных линейно независимы. Для экономических показателей это условие выполняется не всегда. Под мультиколлинеарностью понимается высокая взаимнаякоррелированность объясняющих переменных, которая приводит к линейной зависимости нормальных уравнений. Мультиколлинеарность может возникать в силу разных причин. Например, несколько независимых переменных могут иметь одинаковый временной тренд, относительно которого они совершают малые колебания. Существует несколько способов для определения наличия или отсутствия мультиколлинеарности. Один из подходов заключается в анализе матрицы коэффициентов парной корреляции. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,8. Другой подход состоит в исследовании матрицы Х'Х. Если определитель матрицы Х'Х близок к нулю, то это свидетельствует о наличии мультиколлинеарности. Для устранения или уменьшения мультиколлинеарности используется ряд методов. Наиболее распространенные в таких случаях следующие приемы: исключение одного из двух сильно связанных факторов, переход от первоначальных факторов к их главным компонентам, число которых быть может меньше, затем возвращение к первоначальным факторам. Самый простой из них (но не всегда самый эффективный) состоит в том, что из двух объясняющих переменных, имеющих высокий коэффициент корреляции (больше 0,8), одну переменную исключают из рассмотрения. При этом какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании экономических соображений. Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной. Более сложным приемом в таких случаях является переход от первоначальных факторов к их главным компонентам, число которых быть может меньше, затем возвращение к первоначальным факторам Еще одним из возможных методов устранения или уменьшения мультиколлинеарности является использование стратегии шагового отбора, реализованную в ряде алгоритмов пошаговой регрессии. Наиболее широкое применение получили следующие схемы построения уравнения множественной регрессии: метод включения факторов и метод исключения – отсев факторов из полного его набора. В соответствии с первой схемой признак включается в уравнение в том случае, если его включение существенно увеличивает значение множественного коэффициента корреляции, что позволяет последовательно отбирать факторы, оказывающие существенное влияние на результирующий признак даже в условиях мультиколлинеарности системы признаков, отобранных в качестве аргументов из содержательных соображений. При этом первым в уравнение включается фактор, наиболее тесно коррелирующий с Y, вторым в уравнение включается тот фактор, который в паре с первым из отобранных дает максимальное значение множественного коэффициента корреляции, и т.д. Существенно, что на каждом шаге получают новое значение множественного коэффициента (большее, чем на предыдущем шаге); тем самым определяется вклад каждого отобранного фактора в объясненную дисперсию Y. Вторая схема пошаговой регрессии основана на последовательном исключении факторов с помощью t -критерия. Она заключается в том, что после построения уравнения регрессии и оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение t - статистики. После этого получают новое уравнение множественной регрессии и снова производят оценку значимости всех оставшихся коэффициентов регрессии. Если среди них опять окажутся незначимые, то опять исключают фактор с наименьшим значением t -критерия. Процесс исключения факторов останавливается на том шаге, при котором все регрессионные коэффициенты значимы. Ни одна их этих процедур не гарантирует получения оптимального набора переменных. Однако при практическом применении они позволяют получить достаточно хорошие наборы существенно влияющих факторов. При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а Особым случаем мультиколлинеарности при использовании временных выборок является наличие в составе переменных линейных или нелинейных трендов. В этом случае рекомендуется сначала выделить и исключить тренды, а затем определить параметры регрессии по остаткам. Игнорирование наличия трендов в зависимой и независимой переменных ведет к завышению степени влияния независимых переменных на результирующий признак, что получило название ложной корреляции. Наиболее часто в практических исследованиях возникает вопрос: сколько надо наблюдений для надежного определения параметров регрессии? Выбор числа наблюдений определяется требованиями к точности и надежности оценок параметров. Из требований к точности прогноза и вытекает требование на число наблюдений. Обозначим требуемый размер половины доверительного интервала через Большим препятствием к применению регрессии является ограниченность исходной информации, при этом наряду с указанными выше затрудняющими обстоятельствами (мультиколлинеарность, зависимость остатков, небольшой объем выборки и т. п.) ценность информации может снижаться за счет ее «засоренности», т. е. проявления новых обстоятельств, которые ранее не были учтены. Резко отклоняющиеся наблюдения могут быть результатом либо действия большого числа сравнительно малых случайных факторов, которые в редких случаях приводят к большим отклонениям, либо это действительно случайные один или несколько выбросов, которые можно исключить как аномальные. Однако при наличии не менее трех аномальных отклонений на несколько десятков наблюдений их приписывают наличию одного или нескольких неучтенных факторов, которые проявляются только в виде аномальных наблюдений. [1] Термин "регрессия" (regression (лат.) – отступление, возврат к чему-либо) ввел английский статистик Ф. Гальтон. Он исследовал влияние роста родителей и более отдаленных предков на рост детей. По его модели рост ребенка определяется наполовину родителями, на четверть – дедом с бабкой, на одну восьмую прадедом и прабабкой и т.д. Другими словами, такая модель характеризует движение назад по генеалогическому дереву. Ф. Гальтон назвал это явление регрессией как противоположное движению вперед – прогрессу. В настоящее время термин "регрессия" применяется в более широком плане – для описания статистической связи между случайными величинами.
|

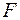 -критерий меньше табличного значения.
-критерий меньше табличного значения.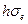 , где
, где 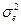 — оценка дисперсий случайной составляющей. Достижение этой желаемой точности определяется как объемом выборки, так и расположением прогностических значений факторов. Чем более разнесены последние от средних выборочных значений, тем меньше точность прогноза.
— оценка дисперсий случайной составляющей. Достижение этой желаемой точности определяется как объемом выборки, так и расположением прогностических значений факторов. Чем более разнесены последние от средних выборочных значений, тем меньше точность прогноза.


