Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные. Определение. Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины:
Для дискретной случайной величины формула начального момента имеет вид:
Для непрерывной случайной величины:
Определение. Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины:
Нетрудно заметить, что при k = 1 первый начальный момент случайной величины Х есть ее математическое ожидание (ν;1 = М (Х)), при k = 2 второй центральный момент – дисперсия (μ;2= D (Х)). Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков. Третий центральный момент μ;3 служит для характеристики асимметрии (т.е. скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на σ;3, где σ; – среднее квадратическое отклонение случайной величины Х. Полученная величина А называется коэффициентом асимметрии случайной величины:
Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен нулю А = 0.
Четвертый центральный момент μ;4 служит для характеристики крутости (островершинности или плосковершинности) распределения. Эксцессом случайной величины называется число
(Число 3 вычитается из отношения потому, что для нормального распределения, которое встречается наиболее часто, отношение μ4/σ4 = 3). Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом.
|

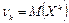 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0). .
.



