Определение операторных характеристик
Для расчета обобщенной характеристики цепи можно применить любые известные методы, например, метод контурных токов, метод узловых напряжений, метод эквивалентного генератора и др. Если сложная цепь содержит только один источник Еi(p), включенный в i-ом контуре, то контурный ток, создаваемый при этом в другом k-ом контуре
где
Минор
и тогда
Поскольку
Решив уравнения N(p) = 0 и M(p) = 0 и разложив N(p) и M(p) на множители, получим
где Таким образом, операторная характеристика может быть задана распределением нулей и полюсов (значений р при которых функция обращается в бесконечность), а также масштабным коэффициентом К. Операторные характеристики цепи удобно использовать при нахождении переходной и импульсной характеристик. Действительно, исходя из определения операторной характеристики, изображение отклика
С другой стороны, изображение отклика цепи на единичную функцию на входе является изображением переходной характеристики
Аналогично, изображение отклика цепи на дельта-функцию является изображением импульсной характеристики
Пример 7. Для электрической цепи, приведенной в примере 1, определить переходную и импульсную характеристики, используя операторную характеристику. Решение. Найдем операторную характеристику цепи (рис. 1.66).
Рис.1.66
где
Подставив значения R, L, C в последнее выражение, получим
отсюда переходная характеристика
и импульсная характеристика
|

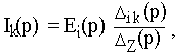
 - определитель системы уравнений, составленных методом контурных токов (в операторной форме);
- определитель системы уравнений, составленных методом контурных токов (в операторной форме);  - алгебраическое дополнение элемента в операторной форме
- алгебраическое дополнение элемента в операторной форме
 равен определителю системы, из которого исключена i-я строка, соответствующая i-ому контуру, где действует ЭДС
равен определителю системы, из которого исключена i-я строка, соответствующая i-ому контуру, где действует ЭДС  , и k-й столбец, соответствующий искомому k-ому току. Следовательно,
, и k-й столбец, соответствующий искомому k-ому току. Следовательно,



 представляют собой полиномы от собственных и взаимных операторных сопротивлений независимых контуров цепи, а сопротивления являются рациональными функциями р с вещественными коэффициентами, любая операторная характеристика линейной цепи
представляют собой полиномы от собственных и взаимных операторных сопротивлений независимых контуров цепи, а сопротивления являются рациональными функциями р с вещественными коэффициентами, любая операторная характеристика линейной цепи  также является рациональной функцией р с вещественными коэффициентами, т. е. может быть представлена в виде отношения двух полиномов
также является рациональной функцией р с вещественными коэффициентами, т. е. может быть представлена в виде отношения двух полиномов

 - масштабный коэффициент;
- масштабный коэффициент;  - нули функции;
- нули функции;  - полюсы функции
- полюсы функции 





 ,
,
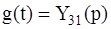 .
.


