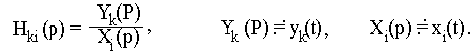Отклик на экспоненциальное воздействие
Операторные характеристики линейных цепей
Во многих случаях воздействующая функция может быть представлена в обобщенной форме
где обобщенная (комплексная) амплитуда обобщенная (комплексная) частота В зависимости от величин, определяющих экспоненциальное воздействие, получается тот или иной закон изменения e(t). Если мнимая часть обобщенной частоты не равна нулю
и характер воздействующей функции зависит от вещественной части а) при
б) при
в) при
если
г) при
д) при
е) при
а г
б д
в е Рис. 1.64
Таким образом, Вследствие того что интегрирование и дифференцирование экспоненциальной функции не изменяет её вида, отклик цепи на данное воздействие является экспоненциальной функцией той же частоты, причем отношение отклика цепи к воздействию в этом случае не зависит от времени.
При
Входное сопротивление пассивного линейного двухполюсника
Полагая s = p, получим выражения для операторных сопротивлений идеализированных элементов цепи, полагая s = jw - выражения для комплексных входных сопротивлений элементов при гармоническом воздействии. Следовательно, оператор преобразования Лапласа можно рассматривать как обобщенную (комплексную) частоту экспоненциального воздействия вида
Понятие об операторных характеристиках Рассмотрим идеализированную линейную цепь, не содержащую независимых источников тока и напряжения (рис. 1.65).
Рис. 1.65
Операторной, или обобщенной, частотной характеристикой
Операторная характеристика линейной цепи численно равна отношению отклика цепи к внешнему воздействию при внешнем воздействии вида
Для перехода от операторной характеристики цепи к её комплексной частотной характеристике (КЧХ) необходимо заменить р на jw, т. е. КЧХ есть частный случай обобщенной частотной характеристики при р = jw. Операторная характеристика цепи определяется только видом цепи и параметрами входящих в неё элементов. Как и КЧХ, операторные характеристики делятся на входные и передаточные. В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве отклика, различают: 1. Операторное входное сопротивление
2. Операторную входную проводимость
3.Операторный коэффициент передачи по напряжению
3. Операторный коэффициент передачи по току
5. Операторное передаточное сопротивление
6. Операторную передаточную проводимость
|

 ,
, и
и  - комплексные числа:
- комплексные числа: ,
, .
. , то
, то
 (рис. 1.64):
(рис. 1.64): ;
; , то
, то  ;
;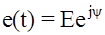 ;
; .
.





 линейной цепи называется отношение операторного изображения отклика цепи Y(p) к операторному изображению внешнего воздействия X(p)при нулевых начальных условиях:
линейной цепи называется отношение операторного изображения отклика цепи Y(p) к операторному изображению внешнего воздействия X(p)при нулевых начальных условиях: