Свойства (теоремы) преобразования Лапласа
Теорема о сложении или линейность преобразования:
Теорема об интегрировании:
Теорема о дифференцировании:
Теорема запаздывания:
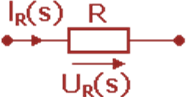
Преобразование Лапласа позволяет получить для резистивного, индуктивного и емкостного элементов соотношения между напряжением и током в операторной форме (рисунке 2).
При расчете переходного процесса операторным методом можно выделить несколько логически самостоятельных этапов: 1) представить исходные данные о параметрах всех элементов схемы цепи в операторной форме. Это означает, что, во-первых, ЭДС источников напряжения и токи источников тока, заданные мгновенными значениями 2) для полученной схемы замещения в операторной форме составить и решить полную систему независимых уравнений по первому и второму законам Кирхгофа в операторной форме, т. е. найти изображение 3) обратным преобразованием нужно найти оригинал Пример. Рассчитаем ток в катушке индуктивности в цепи (рисунок 3), содержащей ЭДС
Для выбранных положительных направлений токов составим одно уравнение по первому закону Кирхгофа для узла «а»:
и два уравнения по второму закону Кирхгофа:
или
Решая систему из 3-х уравнений, получаем
Воспользуемся таблицей преобразований, получим
|
.
.
.
.
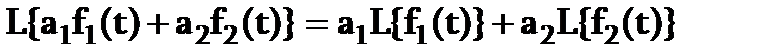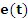и 
, следует представить соответствующими изображениями 
и 
и, во-вторых, пассивные элементы – схемами замещения по рисунку 2;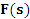
искомой величины, например, ток 
, например, ток 
, и при нулевых начальных условиях.
.
.
