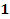Операторный метод расчета переходных процессов
1. Белецкий, А.Ф. Основы теории линейных электрических цепей: учебник / А.Ф.Белецкий. - М.: Связь, 1967.- 607 с. 2. Новгородцев, А.Б. 30 лекций по теории электрических цепей: учебник / А.Б.Новгородцев.- СПб.: Политехник, 1995.- 519 с. 3. Исследование активного RC – фильтра: метод. указания / сост. В.Я.Павлов, Е.В. Козин, В.В. Сергеев, В.А.Филин. – СПб.: Изд-во СПбГУТ, 2002.- 35 с. Операторный метод расчета переходных процессов Идея операторного метода заключается в том, что расчет переходного процесса переносится из области функций действительной переменной (времени t) в область функций комплексного переменного Сначала дифференциальные уравнения преобразуются в алгебраические уравнения (прямое преобразование). Затем полученные алгебраические уравнения решаются относительно неизвестных величин. Полученные решения преобразуются в область действительного переменного (обратное преобразование). Для прямого преобразования функций времени применяется преобразование Лапласа
что сокращенно записывается так:
где
Примем, что начало переходного процесса в цепи соответствует моменту времени Таблица 1 – Изображения функций по Лапласу
|
.
,
,
– функция времени, называемая оригиналом, определена при 
, интегрируема в интервале времени 
и равна нулю при 
;
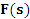– функция комплексного переменного 
, называемая лапласовым изображением.
.
