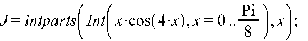Отчёт по НПП.Мэрий города Новосибирска А.Н Лысаков Инспектор ГУБО Мэрий города Новосибирска П.В Заринова Отчёт по НПП.
по теме: Решение определённых интегралов в Maple.
Выполнил: ст. гр. КБ-11 Смирнов И.Ю. Проверил:
Хабаровск 2012 г. Содержание:
1)Задание……………………………………………………..3 2) Реферат……………………………………………………3-5 3) Введение……………………………………………………5 4) Проектная часть ………………………………………….5-12 5) Заключение…………………………………………………12 6) Список используемой литературы ……………………….12
Задание. 1)Построить график подынтегральной функции. 2)Вычислить точное значение (аналитически) используя средства Maple. 3) Вычислить приближённое значение, используя средства Maple. 4) Вычислить приближённое значение, реализовав в Mapleлюбой численный метод для вычисления определённого интеграла.
Реферат. Maple — программный пакет, система компьютерной алгебры. Является продуктом компании Waterloo Maple Inc., которая с 1984 года выпускает программные продукты, ориентированные на сложные математические вычисления, визуализацию данных и моделирование. Система Maple предназначена для символьных вычислений, хотя имеет ряд средств и для численного решения дифференциальныx уравнений и нахождения интегралов. Обладает развитыми графическими средствами. Имеет собственный язык программирования, напоминающий Паскаль. 1)Пожалуй, одно из наиболее впечатляющих свойств программы Maple - превосходная графика. Команды построения графиков и анимации Maple позволяют удовлетворить большинство научных и инженерных потребностей, могут служить прекрасной иллюстрацией в учебном процессе. Программа имеет большое количество функций и опций настроек для построения как двух- так и трехмерных графических объектов. Помимо команд plot и plot3d основной библиотеки имеется несколько специализированных пакетов для этих целей: это прежде всего пакет plots, содержащий около пятидесяти команд для построения различного рода графиков и анимации; вспомогательный пакет plottools, позволяющий создавать различные (около тридцати) дву- и трехмерные графические примитивы, которые могут быть применены в других графиках; пакет stats[statplot]содержащий команды для построения специализированных статистических графиков; пакет DEtools, содержащий команды построения графиков решения дифференциальных уравнений как обыкновенных так и в частных производных, фазовых портретов, полей направлений; и, наконец, геометрический пакет geometry,содержащий команду draw,позволяющую отобразить различные геометрические построения на плоскости.
2) Аналитическое и численное интегрированиe. Неопределенный интеграл прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования; отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int. Команда Int выдает на экран интеграл в аналитическом виде математической формулы. Для вычисления определенного интеграла > Int((1+cos(x))^2, x=0..Pi)= int((1+cos(x))^2, x=0..Pi);
Если в команде интегрирования добавить опцию continuous: int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций. Несобственные интегралы с бесконечными пределами интегрирования вычисляются, если в параметрах команды int указывать, например, x=0..+infinity. Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e), где e – точность вычислений (число знаков после запятой).
3) Основные методы интегрирования. В Maple имеется пакет student, предназначенный для обучения математике. Он содержит набор подпрограмм, предназначенных для выполнения расчетов шаг за шагом, так, чтобы была понятна последовательность действий, приводящих к результату. К таким командам относятся интегрирование по частям inparts и замена переменной changevar. Формула интегрирования по частям:
Если обозначить подынтегральную функцию f=u (x) v’ (x), то параметры команды интегрирования по частям такие:intparts(Int(f, x), u),гдеu– именно та функция u(x), производную от которой предстоит вычислить по формуле интегрирования по частям. Если в интеграле требуется сделать замену переменных x=g (t) или t=h (x), то параметры команды замены переменных такие: changevar(h(x)=t, Int(f, x),t),гдеt - новая переменная. Обе команды intparts и changevarне вычисляют окончательно интеграл, а лишь производят промежуточную выкладку. Для того, чтобы получить окончательный ответ, следует, после выполнения этих команд ввести команду value(%); где %- обозначают предыдущую строку. Не забудьте, перед использованием описанных здесь команд обязательно загрузить пакет student командой with(student).
Введение. В этой работе мы должны изучить основные команды программы Maple и научиться использовать их на практике, так же попробовать создать программу в среде Maple для численного решения определённых интегралов.
Проектная часть. 1)Постройте график подынтегральной функции.
a) >
2) Вычислить точное значение (аналитически) используя средства Maple. a) > >
>
>
>
b) >
>
>
3)Вычислить приближённое значение, используя средства Maple. a)Метод прямоугольника: >
>
>
>
>
>
>
b) Метод Симпсона: >
>
4)Вычислить приближённое значение, реализовав в Mapleлюбой численный метод для вычисления определённого интеграла. a)
> > >
> >
>
>
0.1507044480
Блок-схема метода трапеции:
b)
> > >
> >
>
>
>
0.01625929116
Заключение. В результате этой работы мы изучили основные команды программы Mapleи научились программировать в среде Mapleна начальном уровне.
Список используемой литературы. 1)http://www.exponenta.ru. 2)wikipedia.org. 3)Программирование и разработка приложений Maple (В.З Аладьев, В.К Бойко, Е.А Ровба)
|
вычисляется с помощью 2-х команд: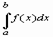
в командах int и Int добавляются пределы интегрирования, например,
