Методы перспективного анализа

 

Современное экономическое прогнозирование насчитывает в своем арсенале большое число разнообразных методов и приемов. Важнейши­ми являются методы прогнозирования на базе динамических рядов. Мы рассмотрим в основном эти методы, учитывая то, что практически на лю­бом предприятии можно построить динамические ряды его экономичес­ких показателей за ряд лет.

Динамический ряд (у) — это ряд наблюдений значений измеряе­мого параметра (и) в последовательные моменты времени (t):

y = f (u_j), i= t_1, t _2…., t _n (1)

Динамический ряд есть частный случай табличной функции, кото­рая представляет собой «протокол» любого наблюдения. Математичес­кая обработка этой таблицы преследует цель «выжать» из нее как можно больше информации о закономерностях развития данного явления в прошлом и настоящем, использовать полученную информацию для ха­рактеристики явления в будущем.

Задача прогнозирования динамических рядов заключается в том, чтобы по имеющимся наблюдениям за ходом экономического процесса в моменты времени t ₁, t ₂, ..., t _n предсказать значения измеряемого пара­метра в моменты времени t _n+1, t _n+2, ...

Несмотря на кажущуюся простоту, данная задача в общем виде для нестационарных процессов еще не решена. Ббльшая же часть эко­номических процессов не стационарна, что выражается наличием в ди­намических рядах эволюторной составляющей — временнбго тренда. Поэтому среди методов прогнозирования динамических рядов большое место занимают всевозможные неформальные, эмпирические методы, базирующиеся на интуиции и опыте специалистов определенной отрасли.

Неформальный подход к анализу позволяет сделать прогнозиро­вание динамических рядов более определенным путем введения в по­становку дополнительных ограничений (условий). В частности, в эконо­мической теории эти условия сформулированы как принципы экономи­ческого прогнозирования.

Перечислим основные принципы экономического прогнозирова­ния.

1. Прогнозируемый экономический показатель (параметр) рассмат­ривается лишь как элемент в сложном клубке (множестве других) взаи­мосвязанных элементов, т.е. как часть единого целого.

2. По отношению к данному элементу всегда можно найти другие, первичные или производные.

3. Изменения экономических показателей, помимо всего прочего, являются предметом сознательного действия людей (общества).

Некоторые из возможных решений, вытекающих из различной сте­пени учета данных принципов, уровня осведомленности лица, делающе­го прогноз, о характере рассматриваемого явления, его квалификации, приводятся ниже.

ПРОГНОЗ В ПРЕДПОЛОЖЕНИИ НЕИЗМЕНЯЕМОСТИ ЗНАЧЕ­НИЙ ПРЕДШЕСТВУЮЩИХ УРОВНЕЙ РЯДА В БУДУЩЕМ. Этот про­гноз осуществляется по формуле: завтра будет то же, что и сегодня. Ма­тематическая запись данного утверждения приводит к ряду неравенств:

Обычно формула (2) применяется не к исходному ряду (1), а к раз­личным его модификациям. Так, применение этой формулы к ряду абсо­лютных приростов приводит к равенствам:

где Δ u _t,— абсолютный прирост уровня в году (t), вычисленный по формуле

Абсолютные приросты, в свою очередь, могут быть вычислены не для исходного ряда (1), а для преобразованного. Например, для кумуля­тивного ряда отклонений фактических уровней ряда (1) от плана, сред­него из исходных уровней или другого уровня, принятого за норму:

 

Δ y _n+1 = Δ y, Δ y _n+2 = Δ y _{n+1, …,}.(4)

где Δy,=y_t –y_t-1, t=2,3,...,n,n+1...;

у_t — кумулятивная сумма в году t, вычисленная по формуле

где ū — нормальный уровень.

ПРОГНОЗ В ПРЕДПОЛОЖЕНИИ НЕИЗМЕНЯЕМОСТИ В БУДУ­ЩЕМ СРЕДНИХ ЗНАЧЕНИЙ ПРЕДШЕСТВУЮЩИХ УРОВНЕЙ. Для ал­горитмов (2) — (4) вычисления прогнозируемых значений ряда (1) непо­средственно учитывается всего одна точка предыстории процесса, хотя необходимой предпосылкой их применения может служить только дли­тельный опыт наблюдения совпадений текущих точек с предшествую­щими, имевшийся в прошлом. Шагом вперед по пути учета в прогнозиро­вании предыстории большей длины (больше одной точки) является использование для этих целей алгоритмов скользящих средних и сред­него темпа роста.

При помощи скользящей средней прогнозируемые значения ряда (1) можно вычислять с учетом двух, трех и более точек предысто­рии. Имеем

При k = п прогнозируемое значение ряда (t) в момент t _n+1, равно среднему арифметическому всех наблюденных значений. При k < n — соответствующему среднему значению ряда из (k) точек, непосред­ственно предшествующих прогнозируемой.

В формуле (5) все точки, участвующие в вычислении средней, имеют равное достоинство (равный вес). Необходимость учета неравных до­стоинств приводит к формуле взвешенной средней:

Научно обоснованным способом взвешивания достоинств исход­ных точек для вычисления прогнозируемых значений является алго­ритм экспоненциальной средней, по которому значения весов х_t по мере отдаления предшествующей точки от прогнозируемой убывают по экспоненте.

На втором этапе в зависимости от конкретных целей дальнейшего использования аналитической формулы в задачу подбора вводят допол­нительные ограничения. Обычно это ограничения по степени приближе­ния (аппроксимации), виду эмпирической функции, поведению ее графи­ка вне заданного интервала наблюдения.

На третьем этапе вычисляют все неизвестные параметры, входя­щие в аналитическую формулу, рассчитывают теоретические уровни ряда, а также показатели соответствия полученной формулы принятым ограничениям. Для определения неизвестных параметров формулы чаще всего используют метод наименьших квадратов.

Пример. Прогнозирование при помощи аналитических формул. Есть следующие данные о спросе на продукцию машиностроительного предприятия:

Требуется составить прогноз на последующие пять лет. Пользуясь изложенной выше методикой, подбор аналитической формулы будем вести по этапам.

Этап 1. Сравнивая полученный графике кривыми различных эмпи­рических функций из математических справочников, определяем наибо­лее подходящие формулы, описывающие исходные данные:

u=a₀+a₁t+a₂t²;

lg u = a₀ + a₁ (lg t) + a₂ (lg t)².

График первой функции — одновершинная парабола (с вершиной в положительной части u, t) с ветвями, уходящими книзу.

График второй функции — кривая, также имеющая вершину в по­ложительной четверти u, t, но с короткой (левой) ветвью, идущей книзу, и правой ветвью, асимптотически приближающейся к оси времени.

Этап 2. Предположим, нам известно из других источников, что спрос на продукцию данного предприятия в будущем имеет тенденцию постепенного уменьшения вплоть до нулевого уровня. Тогда вторая фун­кция лучше подходит для прогностических целей, поскольку поведение ее графика вне интервалов наблюдения больше соответствует характе­ру предполагаемых изменений уровня спроса.

Этап 3. Система нормальных уравнений для функции имеет вид:

Все необходимые суммы удобнее вычислять в таблице (см. с.222).Подставляя соответствующие суммы в исходную систему, получим

16а₀ +13,30а₁ +12,81 а₂ =33,52;

13,30а₀ +12,81а₁ + 12,95а₂ = 27,66;

12,81а₀ +12,95а₁ +13,49а₂ =26,40.

Решение этой системы дает а₀ = 1,98; а₁ = 0,84; а₂ = - 0,72. Значит, окончательная эмпирическая формула для расчета теоретических уров­ней имеет вид

Подставляя в нее значения Ig t и (Ig t)² (t = 1,2,..., 16) и потенциируя полученные выражения, можно найти соответствующие уровни для u (таблица на с. 223—224). Для сравнения в этой таблице приведены так­же результаты вычисления теоретических уровней по параболе второго порядка: u=99,8+16,6 t -1 ,2t².

Прогнозируемые значения уровней по параболе второго порядка в соответствующие моменты времени составили:

для t =17—u17=35;

для t =18—u18=19;

для t =19—u19=-18;

для t =20—u20=-48;

для t =21—u21=-82.

Ясно, что экономически такой прогноз ввиду отрицательности u19, u20, u21 интерпретировать невозможно.

МОДЕЛЬ РЕГРЕССИОННОГО ПРОГНОЗА. Модель регрессион­ного прогноза — широко известный метод, при котором прогнозируемое значение u_k рассматриваемого показателя в моменты t_n+1, t_n+2... пред­ставляется как функция а факторов u₁, u₂,..., u_a:

где k = n+1, n+2,...

При а= 1 имеем однофакторную модель. Формулу (8) можно рас­сматривать как однофакторную, где единственным фактором является время. При наличии более одного фактора модель называется много­факторной. Вид функции (9) и значения параметров, входящих в анали­тическую формулу, определяются по предыстории процесса.

Прогнозы по регрессионным моделям более надежны, поскольку они позволяют проводить эксперименты на моделях, в которых учитыва­ется большее число факторов, влияющих на развитие процесса. Кроме того, полученные результаты всегда легко объяснить и обосновать. В си­лу этих причин прогнозы по уравнениям регрессии (иначе их называют производственными функциями) используются практически при эконо­мическом прогнозировании всех видов: макро- и микро-, краткосрочном и долгосрочном, частном и общем и т.д.

ПРОГНОЗИРОВАНИЕ МЕТОДОМ ВЫДЕЛЕНИЯ СОСТАВЛЯЮ­ЩИХ ВРЕМЕННОГО РЯДА. Все большее применение в экономическом прогнозировании (особенно в краткосрочном) находит метод, при кото­ром прогнозируемое значение рассматриваемого показателя в моменты времени t_n+1, t_n+2, ... определяется как итог прогнозов двух (либо трех) со­ставляющих. Имеем

U_k = c_k + w_k + a_k. (10)

где k=n+1, n+2,...,

или

u _k = c_k + w_k +а _k +а _k (П)

где с_k — прогнозируемое значение постоянной составляющей (тренда), образую­щегося под влиянием комплекса постоянно действующих на протяжении длительного времени факторов;

w_k — прогнозируемое значение периодической составляющей, образующей­ся под влиянием комплекса периодически действующих факторов (се­зонность, цикличность хозяйственных операций и пр.);

а_k — прогнозируемое значение автокорреляционной составляющей в случае корреляции значений двух смежных членов исходного динамического ряда;

a_k —значение случайной составляющей.

Модель (11) более полная по сравнению с моделью (10). Прогнозы для составляющих с_k и w_k могут быть получены по моделям (8) и (9). Уравнение автокорреляции для нахождения прогнозируемого значения соответствующей составляющей в принципе не отличается от форму­лы (9) при линейности вида функции f = (u₁^k, u₂^k, …, u_a^k), кроме того, что в

качестве факторов u₁, u₂, ..., u_a рассматриваются значения а членов ис­ходного динамического ряда.

Опыт показывает, что применение в экономике многих математи­ческих методов прогнозирования, дающих удовлетворительные резуль­таты в других отраслях науки и техники, часто не оправдывается. Анализ информационного содержания изложенных математических подходов показывает, что существенный момент в них — использование для про­гнозирования в явном виде только прошлой информации. Этого недо­статочно при составлении экономических прогнозов.

В задачах прогнозирования результатов хозяйственной деятель­ности промышленного предприятия (прогнозы выполнения плана выпу­ска, реализации и т.п.) возникает необходимость учета не только про­шлого опыта, предыстории рассматриваемого процесса, но и ряда новых факторов: плановых данных, данных аналогичных процессов, развиваю­щихся с опережением по отношению к рассматриваемому процессу (на­пример, необходимость учета опережающего развития промышленно­сти строительных материалов по отношению к строительству); новые элементы в механизме явления, обычно проявляющиеся в последний момент, предшествующий прогнозируемому периоду, и действующие как ускорители, которые обеспечивают перелом в направлении сложив­шейся тенденции в будущем. Обычно эта информация уже имеется к на­чалу составления прогнозов и может быть учтена при помощи следую­щей экономико-математической модели (метод трех параметров).

Минимизируем функционал:

где х_i — исходный динамический ряд, k последних точек которого являются пла­новыми или заменяющими план данными;

y_i — сглаженный динамический ряд, k последних точек которого являются прогнозом;

с_i — тренд, найденный по прошлым (отчетным) значениям и экстраполиро­ванный на k точек вперед.

В выражении для λ первое слагаемое измеряет эвклидову бли­зость искомой точки к исходному ряду, второе — близость к линии тренда, третье — близость к линейному дрейфу, образуемому за счет уров­ней трех последних точек отчетного периода.

Минимум функционала λ находят обычными математическими средствами в результате решения системы линейных уравнений вида

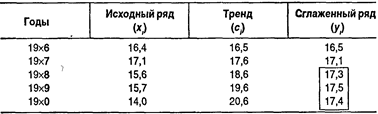
В таблице для примера приводятся результаты прогнозирования объема реализации продукции промышленного предприятия методом трех параметров. В качестве прогноза рассматриваются три последних точки сглаженного ряда (обведены прямоугольником), годы 19х8,19х9, 19х0.

Во второй графе в качестве исходного ряда представлены отчет­ные данные по предприятию за 19х0—19х7 гг. и плановые значения на 19х8—19х0 гг. В третьей графе приведены значения тренда, найденного из линейной зависимости с_i = 10,3+ t пo отчетным данным предприятия и экстраполированного на плановые годы.

В заключение следует отметить, что применение математических методов в анализе экономической перспективы позволяет доводить тео­ретические построения до количественных вычислений.