Предположения, лежащие в основе модели линейного программирования

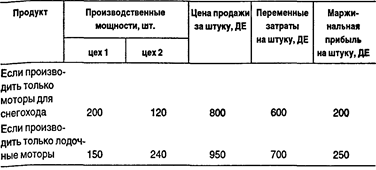
Ранее была продемонстрирована важность фактора ограниченно­сти ресурсов для принятия решения об ассортименте продукции. Наиболее выгодный (прибыльный) продукт — это не всегда продукт с наивыс­шей маржинальной прибылью на изделие. Наоборот, наиболее прибыль­ный продукт — это тот, который приносит наибольшую прибыль на еди­ницу ограничивающего ресурса или ограничивающего фактора, напри­мер такого, как имеющиеся суммарные машино-часы. На практике обычно существует более чем одно ограничение. Следовательно, про­блема заключается в максимизации суммарной маржинальной прибыли при данном множестве ограничений. Модель линейного программирова­ния (ЛП) используется при решении проблем, где предположение о ли­нейности является приемлемым.

Применяя модель ЛП, мы предполагаем, что только один фактор — объем выпуска — вызывает изменение в суммарных затратах на продук­цию. Все прочие затраты предполагаются фиксированными. Для многих краткосрочных решений это предположение достаточно приемлемо. Там, где это предположение неприемлемо, прибегают к другим моделям.

Пример. Определение оптимального ассортимента продукции. Компания производит моторы. На ее заводе собирают и испытывают мо­торы двух видов — для снегоходов и для лодок (подвесной). Каждая модель проходит два подразделения — цех сборки и цех контроля и испытаний.

Исходные данные:

Предположим, что цех работает с мотором одного вида. Из таблицы вид­но, что цех сборки может собирать максимум 200 моторов для снегоходов (300 машино-ч: 1,5 машино-ч/шт. = 200 шт.) или 150 шт. для лодок (300 маши-но-ч: 2,0 машино-ч /шт. = 150 шт.). Аналогично цех контроля и испытаний мо­жет протестировать 120 моторов для снегоходов (120 шт.: 1 ч = 120 шт.) или 240 лодочных моторов (120 шт.: 0,5 ч = 240 шт.).

Обобщим эти и другие релевантные данные. Отметим, что по моторам для снегоходов маржинальная прибыль на штуку составляет 200 ДЕ, а по ло­дочным моторам — 250 ДЕ на один мотор.

Известно также, что недостаток (некомплектность) исходных материа­лов для лодочных моторов будет ограничивать их производство до 126 мото­ров в день. Сколько моторов каждого вида должно быть произведено еже­дневно, чтобы получить максимальную прибыль?