Основные определения, поточечная сходимость
Если функция /(х) - нечетная, то коэффициенты ряда (3):
п Ряды Фурье периода 2£ Если функция f(x), удовлетворяет условиям Дирихле в интервале (-С;С) длины 2 С, то в точках непрерывности функции, принадлежащих этому интервалу, справедливо разложение
пл х,. плх п=\
cos---- -dx (л = 0,1,2,...),
•sin------- dx (л =1,2,...). Основные определения, поточечная сходимость Опр.: функциональной последовательностью Пример: при при и т. д.
Опр.: функция
Опр.: функциональным рядом на множестве X, называется выражение вида Опр.: суммой функционального ряда называется функция
|

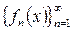 на множестве X, называется последовательность, где каждому числу
на множестве X, называется последовательность, где каждому числу 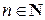 ставится в соответствие по определённому закону некоторая функция
ставится в соответствие по определённому закону некоторая функция 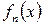 . При этом для фиксированного значения
. При этом для фиксированного значения 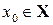
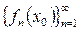 - есть обычная числовая последовательность.
- есть обычная числовая последовательность.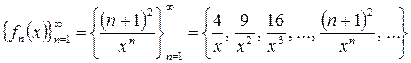
 имеем функцию
имеем функцию  ,
,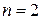 имеем функцию
имеем функцию  ,
,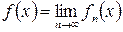 называется предельной функцией для
называется предельной функцией для 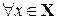 и
и 
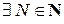 , такое что
, такое что 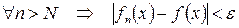 или, как ещё говорят, имеет место поточечная сходимость
или, как ещё говорят, имеет место поточечная сходимость 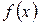 .
.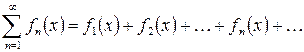 , где функции
, где функции  - обычный числовой ряд.
- обычный числовой ряд.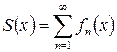 , определённая на X, такая что
, определённая на X, такая что  .
.


