Свойства равномерно сходящихся рядов.
Теорема 1 (о непрерывности): сумма равномерно сходящегося функционального ряда (предел равномерно сходящейся функциональной последовательности) непрерывных функций является непрерывной функцией. Без док-ва.
Теорема 2 а (об интегрировании последовательностей): пусть Без док-ва.
Теорема 2 b (об интегрировании рядов): пусть Без док-ва.
Теорема 3 а (о дифференцировании последовательностей): пусть Без док-ва.
Теорема 3 b (о дифференцировании рядов): пусть Без док-ва.
Замечание 1: в условии теорем нельзя заменить равномерную сходимость на поточечную. Замечание 2: равномерной сходимости не достаточно для дифференцируемости, например для
|

 на
на  и
и  интегрируемы на
интегрируемы на  . Тогда
. Тогда 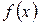 тоже интегрируема на
тоже интегрируема на  .
. на
на 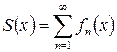 . Тогда
. Тогда  тоже интегрируема на
тоже интегрируема на  .
. и
и  на
на  , такой что
, такой что  поточечно сходится к
поточечно сходится к  , то
, то 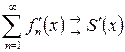 на
на 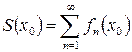 , то
, то 
 , замечаем, что
, замечаем, что  расходится
расходится  (
( ).
).


