Дифференциальные уравнения движения Эйлера
Рассмотрим установившийся поток идеальной жидкости. Как уже говорилось, она не обладает вязкостью, т. е. движется без трения. Как и при выводе дифференциальных уравнений равновесия Эйлера, выделим в потоке элементарный параллелепипед объемом dV = dx dy dz, ориентированный относительно осей координат (см. рис. 2). Проекции на оси координат сил тяжести и давления, действующих на параллелепипед, составляют; для оси х,
для оси у
для оси z
Согласно основному принципу динамики, сумма проекций сил, действующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение. Масса жидкости в объеме параллелепипеда
Если жидкость движется со скоростью w, то ее ускорение равно
или после сокращения
где, согласно уравнению (28a), приведенному на стр. 40, субстанциональные производные соответствующих составляющих скорости равны
Система уравнений (46) с учетом выражений (47) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для установившегося потока. При неустановившемся движении скорость жидкости изменяется не только при перемещении частицы потока из одной точки пространства в другую, но и с течением времени в каждой точке. Поэтому, в соответствии с уравнением (28), составляющие ускорения в уравнении (46), выражаемые субстанциональными производными для неустановившихся условий, имеют вид:
Система уравнений (46) с учетом выражений (47а) представляв собой дифференциальные уравнения движения идеальной жидкости Эйлера для неустановившегося потока.
|





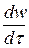 , а проекции ускорения на оси координат:
, а проекции ускорения на оси координат:  ,
, 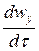 и
и  , где wx, wy и wz – составляющие скорости вдоль осей х, у и z. Разумеется, при этом соответствующие производные по времени не означают изменений во времени составляющих скорости в какой-либо фиксированной точке пространства. Такие изменения
, где wx, wy и wz – составляющие скорости вдоль осей х, у и z. Разумеется, при этом соответствующие производные по времени не означают изменений во времени составляющих скорости в какой-либо фиксированной точке пространства. Такие изменения  ,
,  и
и 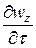 равны нулю в рассматриваемом случае установившегося потока. Производные же
равны нулю в рассматриваемом случае установившегося потока. Производные же 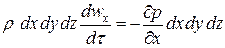
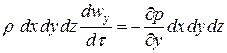


 (46)
(46)
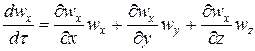
 (47)
(47)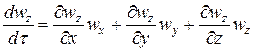

 (47)
(47)



