Дифференциальные уравнения движения Навье–Стокса
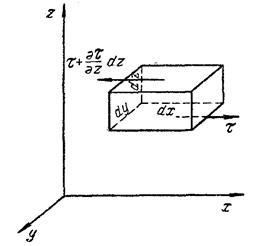
При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения. Действие сил трения Т на выделенный в потоке вязкой жидкости элементарный параллелепипед (рис. 14) проявляется в возникновении на его поверхности касательных напряжений В. этих условиях касательные напряжения возникают лишь на поверхностях dF верхней и нижней граней элементарного параллелепипеда, причем dF = dx dy. Если касательное напряжение на нижней грани параллелепипеда равно
Рис. 14. К выводу уравнений Навье–Стокса
Производная Указанные на рис. 14 стрелками направления сил трения, приложенных к параллелепипеду на его нижней и верхней гранях, обусловлены, например, тем, что более медленные вышележащие слои жидкости затормаживают слой, в котором находится параллелепипед, а более быстрые нижележащие слои «разгоняют» его (вспомним, что на стр. 26 мы условились проводить нормаль к поверхностям соприкосновения перемещающихся относительно друг друга слоев в направлении уменьшения их скорости). Тогда проекция равнодействующей сил трения на ось х
Подставив в это выражение значение касательного напряжения
В более общем случае трехмерного потока составляющая скорости wx будет изменяться не только в направлении z, но и в направлениях всех трех осей координат. Тогда проекция равнодействующей сил трения на ось х примет вид
Сумму вторых производных по осям координат называют оператором Лапласа;
Следовательно, проекция равнодействующей сил трения на ось х может быть представлена как
Соответственно проекции равнодействующей сил трения: на ось у
на ось z
Проекции на оси координат равнодействующей всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости (с учетом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют: на ось х
на ось y
на ось z
Суммы проекций сил на оси координат, в соответствии с основным принципом динамики, должны быть равны произведению массы жидкости r dx dy dz (r — плотность жидкости), заключенной в элементарном объеме, на проекции ускорения на оси координат. Поэтому, приравнивая проекции равнодействующей произведениям массы на проекции ускорения, после сокращения на dx dy dz, получим
где соответствующие субстанциональные производные выражены для установившегося и неустановившегося потоков, уравнениями (47) или (47а). Уравнения (48) представляют собой уравнения Навье – Стокcа, описывающие движение вязкой капельной жидкости. Левые части уравнений (48) выражают произведение массы единицы объема р на проекцию ее ускорения, т. е. представляют собой проекции равнодействующей сил инерции, возникающих в движущейся жидкости. В правых частях тех же уравнений произведение pg отражает влияние сил тяжести, частные производные При движении идеальной жидкости, когда силы трения отсутствуют, при подстановке m = 0 в уравнения (48) последние совпадают с уравнениями (46), т. е. уравнения движения Эйлера можно получить как частный случай уравнений Навье–Стокса. Полное описание движения вязкой жидкости в его наиболее общей форме возможно путем решения уравнений Навье—Стокса совместно с уравнением неразрывности потока. Однако уравнения Навье—Стокса не могут быть решены в общем виде. Получены решения этой сложной системы уравнений только для некоторых частных случаев. Так, для установившегося ламинарного движения жидкости решение уравнений Навье— Стокса позволяет вывести уравнение Пуазейля, полученное выше другим способом. В большинстве же наиболее важных для промышленной практики случаев применение уравнений Навье–Стокса становится возможным либо при ряде упрощающих допущений, либо при преобразовании этих уравнений методами теории подобия.
|

 . Рассмотрим первоначально относительно простой случай одномерного плоского потока капельной жидкости в направлении оси х, когда проекция скорости wx зависит только от расстояния z до горизонтальной плоскости отсчета.
. Рассмотрим первоначально относительно простой случай одномерного плоского потока капельной жидкости в направлении оси х, когда проекция скорости wx зависит только от расстояния z до горизонтальной плоскости отсчета.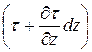 .
.
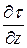 выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда, а
выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда, а  представляет собой изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.
представляет собой изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.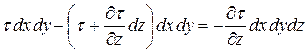
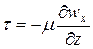 , где
, где  — вязкость жидкости], получим
— вязкость жидкости], получим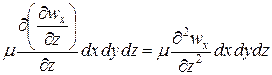
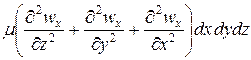
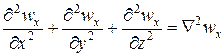
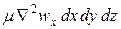
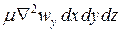
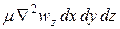
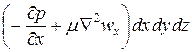
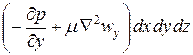




 ,
,  и
и  — влияние изменения гидростатического давления, а произведения вязкости на сумму вторых производных проекций скорости – влияние сил трения на движущуюся жидкость.
— влияние изменения гидростатического давления, а произведения вязкости на сумму вторых производных проекций скорости – влияние сил трения на движущуюся жидкость.


