Пятый расчет
Все показатели фактические 1000 • 290 • 6,8 • 1.6 =3155,2 у.е. Далее сделаем анализ влияния факторов на объем продаж. Отклонение фактического объема продаж от планового произошло за счет влияния следующих факторов: 1) увеличения количества рабочих определяется путем вычитания из второго расчета первого 3115,4 - 2803,8 = +311,6 у.е.; 2) уменьшения числа отработанных дней - из третьего вычитается второй результат 3001,5-3115,4=-113,9у.е.; 3) уменьшения средней продолжительности рабочего дня - из четвертого вычитается третий 2958,0-3001, 5 =-43,5 у.е.; 4) повышения средней часовой выработки 3155,2-2958.0 =+197,2 у.е.. Общее отклонение 3155,2 - 2803,8 = +351,4 у.е. Или 311,6 - 113,9 - 43,5 + 197,2 = +351,4. При использовании МЦП очень важно обеспечить строгую последовательность подстановки: сначала выявляется влияние количественных показателей, а потом - качественных. К качественным относятся, например, выработка, производительность труда, цена. 4.4. Факторный анализ с применением ЭВМ Факторный анализ — это процедура установления силы влияния факторов на функцию или результативный признак (полезный эффект машины элементы совокупных затрат, производительности труда и т.д.) с целью ранжирования факторов для разработки плана организационно-технических мероприятий по улучшению функции. Применение методов факторного анализа требует большой подготовительной работы и трудоемких по установлению моделей расчетов. Поэтому без ЭВМ не рекомендуется применять методы корреляционного и регрессионного анализа, главных компонент. К тому же в настоящее время для ЭВМ различных классов имеются стандартные программы по этим методам. В свою очередь пользоваться установленными с помощью ЭВМ моделями очень просто. На подготовительной стадии факторного анализа большое внимание следует уделять качеству матрицы исходных данных для ЭВМ. С этой целью сначала рекомендуется на основе логического анализа определять группы факторов, влияющих на исследуемую функцию. К исходным данным предъявляются следующие требования: а) в объем выборки должны включаться данные только по однородной совокупности объектов анализа, т.е. одного назначения и класса, используемых (изготавливаемых, функционирующих) в аналогичных условиях по характеру и типу производства, режиму работы, географическому району и т.д. В том случае, когда необходимо увеличить размер матрицы, исходные данные отдельных объектов могут быть приведены в сравнимый вид с большинством объектов по отличающимся признакам путем умножения их на корректирующие коэффициенты; б) период динамического ряда исходных данных должен быть небольшим, но, по возможности, одинаковым для всех объектов. Устойчивый период упреждения (зона прогноза) обычно в два и более раза меньше периода динамического ряда. Например, по данным за 1985-1995гг. можно разработать прогноз до 2000г., а в последующие годы по фактическим данным модель должна обновляться (уточняться); в) исходные данные должны быть качественно однородными, с небольшими интервалами между собой; г) следует применять одинаковые методы или источники формирования данных. Если динамический ряд имеет крупные структурные сдвиги (например из-за изменения цен, ассортимента выпускаемой продукции, программы ее выпуска и т.д.), то все данные должны быть приведены в сравнимый вид или одинаковые условия; д) отдельные исходные данные должны быть независимы от предыдущих и последующих наблюдений. Например, наблюдение не должно определяться расчетным путем по предыдущему наблюдению. Основные параметры корреляционно-регрессионного анализа в связи с их сложностью не приводятся, поскольку все расчеты предполагается выполнять на ЭВМ по стандартной программе. Конечные результаты расчета выдаются на печать (табл. 4.3). Таблица 4.3 Основные параметры корреляционно-регрессионного анализа
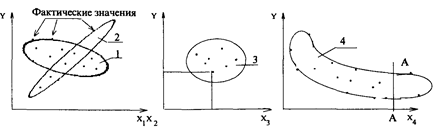
Факторный анализ следует проводить в следующей последовательности: 1. Обоснование объекта анализа, постановка цели. 2. Сбор исходных данных и их уточнение в соответствии с ранее описанными требованиями. 3. Построение гистограмм по каждому фактору с целью определения форм распределения случайных наблюдений. Построение по каждому фактору корреляционных полей, т.е. графическое изображение функций от фактора с целью предварительного определения тесноты и формы связи между функцией и каждым фактором. Примеры корреляционных полей показаны на рис. 4.2.
Рис. 4.2. Примеры корреляционных полей Корреляционные поля построены по исходным статистическим данным X1 — Х4 (факторы) и Y (функция). Анализ корреляционных полей показывает, что: а) между Y и X4 теснота связи слабая, по форме она линейная, обратно пропорциональная; б) между Y и Х1 теснота связи высокая, по форме она линейная, прямо пропорциональная; в) между Y и Х3 связи нет, т.к. функцию Y = f(X3) можно провести в любом направлении; г) между Y и Х4 теснота связи высокая, форма связи — гиперболическая, после линии А—А фактор Х4 на Y уже не оказывает влияния. 4. Составление матрицы исходных данных производится по следующей форме:
и т. д. В матрицу исходных данных следует включать факторы, имеющие примерно такую форму связи, как Y с X1 и Х2 на рис. 4.2. Фактор Х3 с Y не имеет связи, поэтому этот фактор не следует включать в матрицу, фактор Х4 тоже не следует включать в матрицу, поскольку после линии А—А этот фактор влияния на Y не оказывает. Влияние подобных факторов на Y следует учитывать при помощи коэффициентов, определяемых отдельно для каждого фактора и группы предприятий. Наши исследования показывают, что к организационным факторам, имеющим с экономическими показателями гиперболическую форму связи, относятся уровень освоенности продукции в установившемся производстве, программа ее выпуска и др. 5. Ввод информации и решение задачи на ЭВМ. В экономических исследованиях для многофакторных регрессионных моделей чаще всего приемлемы две формы связи факторов с функцией: линейная и степенная. Для двухфакторных моделей применяются также гиперболическая и параболическая формы связи. 6. Анализ уравнения регрессии и его параметров в соответствии с требованиями, изложенными в табл. 4.3. 7. Составление матрицы исходных данных для окончательной модели и решение ее на ЭВМ. Апробация окончательной модели путем подстановки в нее фактических данных по одной из строк матрицы и сравнение полученного значения функции с ее фактическим значением. При составлении новых матриц исходных данных из них исключаются поочередно: а) один из двух факторов, коэффициент частной корреляции между которыми значительно больше коэффициентов парной корреляции между функцией и этими факторами. Например, если между двумя факторами коэффициент частной корреляции равен 0,95, а коэффициенты парной корреляции между функцией и этими факторами равны 0.18 и 0,73, то первый фактор с коэффициентом парной корреляции, равным 0,18, из матрицы можно исключить; б) факторы с коэффициентами парной корреляции между ними и функцией менее 0,1; в) только после соблюдения требований а) и б) исключаются из матрицы факторы, имеющие с функцией обратную, с точки зрения экономической сущности, связь. Например, с повышением сменности работы цеха (фактор) должна расти его годовая производительность (функция). Обратная же зависимость между ними свидетельствует о нерегулярном и недостоверном учете коэффициента сменности, а возможно, и производительности оборудования, либо о неправильной методике расчета этих показателей. Поэтому в этом случае фактор необходимо исключить из матрицы исходных данных и изучать систему учета. Из матрицы могут быть исключены также отдельные строки по предприятиям (периодам), не отвечающие ранее описанным требованиям. Параметры окончательного уравнения регрессии должны отвечать требованиям табл. 4.3. Если невозможно этого достигнуть, модель для ранжирования факторов и прогнозирования экономических показателей не может быть использована. Она пригодна только для предварительного отбора факторов. 8. И последнее — ранжирование. Ранжирование факторов осуществляется по показателю их эластичности. Фактору с наибольшим коэффициентом эластичности присваивается первый ранг, и он является важнейшим. Например, если два фактора имеют коэффициенты эластичности, равные 0,35 и 0,58, то второму фактору нужно отдать предпочтение перед первым при распределении ресурсов на улучшение данной функции (при улучшении второго фактора на 1% функция улучшается на 0,58%, а по первому фактору — 0,35%). Нами проведены специальные исследования зависимостей между элементами затрат и организационными факторами (программа выпуска продукции, уровень ее освоенности, тенденция роста производительности труда). Результаты исследований показали, что эти факторы на экономические показатели оказывают влияние только в определенных границах по гиперболической форме связи. Поэтому эти факторы не должны включаться в общую многофакторную модель, их влияние на функцию должно учитываться отдельно. Например, себестоимость продукции прогнозируется по формуле З = Зр · Кm · Косв · Кпрt (4.2) где 3 — прогнозное значение себестоимости продукции, рассчитанное с учетом организационных факторов производства и технических параметров конструкции; Зр — прогнозное значение себестоимости продукции, рассчитанное по ее техническим параметрам; Кm — коэффициент, учитывающий влияние на себестоимость изменения программы выпуска нового изделия по сравнению с программой выпуска базового (или группы аналогичных проектируемому) изделия. Для изделий массового выпуска этот коэффициент равен единице; Косв — коэффициент, учитывающий влияние на себестоимость уровня освоенности конструкции изделия; Кпрt — коэффициент, учитывающий закономерность неуклонного роста производительности труда. Он определяется по формуле
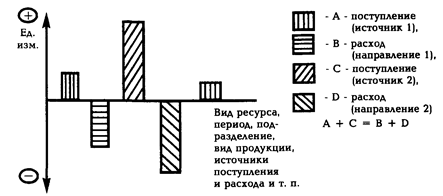
где ΔП — среднегодовой (за последние 5 лет) прирост производительности труда на предприятии (по общему объему продаж); α — доля фонда заработной платы в себестоимости продукции, доли единицы; t — интервал времени в годах, разделяющий периоды выпуска базовой и новой продукции. Анализ применения регрессионных моделей показывает, что в общем случае с повышением коэффициента множественной корреляции улучшаются другие параметры модели. Однако между коэффициентом множественной корреляции и ошибкой аппроксимации не наблюдается устойчивой связи. Покажем это на примере. Для ранжирования факторов, например, влияющих на годовые затрать! на эксплуатацию и ремонты воздушных поршневых компрессоров в условиях ряда машиностроительных предприятий Краснодарского края, окончательно были установлены следующие зависимости: Y1 = 25,7 + 1,53X6 – 0,158X7 – 4,09X8 + 0,0223X9, Y1 = 0,91X60.967 · X7–0.817 · X8–1,525 · X90.065 где Y1 — годовые затраты на эксплуатацию и ремонт воздушных поршневых компрессоров в условиях краснодарских машиностроительных заводов, у.е.; X6 — годовая производительность компрессора, м3; Х7 — уровень централизации изготовления запасных частей к компрессорам, %; X8 — средний разряд рабочих, обслуживающих эти компрессоры; X9 — возраст компрессоров на 01.01.1995 г. (по дате их изготовления), лет. Структура затрат в данном примере: около 60% — энергия и топливо, 25 — заработная плата, 6 — амортизация, 6 — ремонты (без энергии и заработной платы), 3% — вспомогательные материалы. Для обоих уравнений коэффициенты множественной корреляции равны 0,95. Ошибка аппроксимации для линейной формы связи равна ±21,4%, а для степенной ±11,5%. Вторая модель почти в два раза точнее первой, хотя коэффициенты корреляции одинаковы. Коэффициенты эластичности факторов по этим уравнениям отличаются незначительно: для линейной формы связи соответственно 0,900; 0,980; 1,630; 0,060, а для степенной — 0,967; 0,817; 1,525 и 0,065. Между коэффициентами корреляции и эластичности тоже отсутствует устойчивая связь. Регрессионные модели могут также применяться для установления факторов, оказывающих влияние на различные экономические показатели. Факторный анализ может проводиться и без ЭВМ (см. п. 4.7). 4.5. Балансовые методы Балансовый метод предполагает сопоставление взаимосвязанных показателей хозяйственной деятельности с целью выяснения и измерения их взаимного влияния, а также подсчета резервов повышения эффективности производства. При применении балансового метода анализа связь между отдельными показателями выражается в форме равенства итогов, полученных в результате различных сопоставлений. Балансы составляются по различной форме, например: 1) в табличной форме: по вертикали заносятся поступления (доходы), а по горизонтали — распределения (расходы) — табл. 4.4; 2) в табличной форме: по вертикали сначала заносятся активы (за определенный период), ниже — пассивы или обязательства; или слева — актив, справа — пассив; 3) в табличной форме: по вертикали — источник (район, предприятия-поставщики), по горизонтали — район вывоза (предприятия или подразделения-потребители); 4) в графической форме: с плюсом — экономия, с минусом — потери (рис. 4.3) Таблица 4.4 Укрупненный баланс доходов и расходов работника за месяц (пример условный)
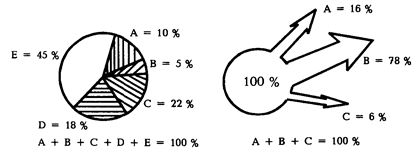
Анализ данных табл. 4.4 показывает, что месячный доход работника составляет 80 у.е. Структура дохода: 47% — зарплата по основному месту работы, 35% — зарплата по совместительству и 18% — гонорар. Структура расходов: 54% — на питание (примерно в 6 раз хуже оптимального), 22% — на квартплату и обустройство жилья, 18% — на одежду, 6% — на отдых.
Рис. 4.3. Виды графических аналитических балансов Графические балансы могут применяться для предварительного анализа структуры распределения, а также для обеспечения наглядности окончательного баланса. Балансовые методы менеджмента — наиболее распространенные. При решении почти любой задачи, по любой функции управления, любого объема необходимо считать приход и расход, прибыль и затраты, поступление и распределение и т.д. Однако в настоящее время балансовым методам менеджмента (как и многим другим) не уделяется необходимого внимания. В табл. 4.5 приведена классификация балансов. Классификация позволяет рассмотреть объект с разных сторон, исследовать его глубже, что является одним из требований менеджмента. Таблица 4.5
|

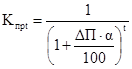 (4.3)
(4.3)