Нахождение арифметического корня натуральной степени с заданной точностью.Пусть требуется найти с точностью ε значение Известен следующий рекуррентный (итерационный) процесс нахождения членов последовательности t0, t1, t2, …, где
При этом оказывается [4], что полученная последовательность сходится при любом t0 >0 к точному значению Удобно в качестве t0 брать значение Итерационный процесс нахождения очередного приближения к величине корня прекращается, как только выполнится неравенство Пример 5. Найти Решение. Здесь a = 1,25, ε = 10-6. Пусть t0 = 1,1 (т.к. 1,12≈1,25). Из формулы (6) при m = 2 имеем:
Значит Аналогично вычисляем t2 = 1,1180339…; Значит,
|
, где a>0, m – натуральное.
, n = 0, 1, 2, …. (6)
. При этом 
с точностью ε;.
с точностью ε = 0,000001 (или ε = 10-6).
, n = 0, 1, 2, ….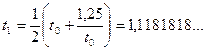
. Так как требуется найти значение корня с точностью ε = 10-6, т.е. с шестью верными значащими цифрами после запятой, при вычислении t1 количество цифр после запятой берем с запасом (например, семь цифр).
. Продолжаем итерационный процесс: t3 = 1,1180339…. Итак, на третьем шаге (итерации) результат в требуемых знаках (шесть цифр после запятой) повторился, т. е. 
.
с точностью 10-6.
