Алгоритм приближенного вычисления корня методом касательных.
Исходные данные: f (x) – функция; f ‘(x) – производная заданной функции f (x); ε; – требуемая точность; x0 – начальное приближение. Результат: xпр – приближенный корень уравнения f (x) = 0. Метод решения: Рассмотрим случай, когда Проведем касательную к кривой y = f (x) в точке В0(b; f(b)). В курсе алгебры выводится уравнение касательной. Уравнение касательной в точке В0 имеет вид Получаем рекуррентную формулу вычисления приближений к корню:
Рис. 8. Геометрическая интерпретация метода касательных для случая
Обратим внимание, что в этом случае в качестве начального приближения к корню выбираем точку x0 = b. Приближение к коню происходит с правой стороны, поэтому получаем приближенное значение корня с избытком. Пусть теперь
   
Рис. 9. Геометрическая интерпретация метода касательных для случая
Если снова провести касательную к кривой в точке В0, то она пересечет ось Ох в точке не принадлежащей отрезку Получаем рекуррентную формулу вычисления приближений к корню, аналогичную первому случаю:
В данном случае в качестве начального приближения к корню выбираем точку x0 = a. Приближение к коню происходит с левой стороны, поэтому находим приближенное значение корня с недостатком. Заметим, что вычислительные формулы метода отличаются друг от друга только выбором начального приближения: в первом случае за x0 принимаем конец b отрезка, во втором – конец a. Убедитесь сами, что при выборе начального приближения корня можно руководствоваться правилом: за исходную точку следует выбрать тот конец отрезка Условие окончания вычислительного процесса:
|

 , т.е.
, т.е.  и
и 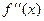 имеют одинаковые знаки. Тогда возможны два случая построения кривой на отрезке
имеют одинаковые знаки. Тогда возможны два случая построения кривой на отрезке  (рис 8).
(рис 8). . В качестве очередного приближения к корню уравнения берем точку пересечения касательной с осью Оx. Полагая y = 0, найдем
. В качестве очередного приближения к корню уравнения берем точку пересечения касательной с осью Оx. Полагая y = 0, найдем  . Теперь
. Теперь  . Применяя метод еще раз для отрезка
. Применяя метод еще раз для отрезка  , получим
, получим  .
. (3)
(3)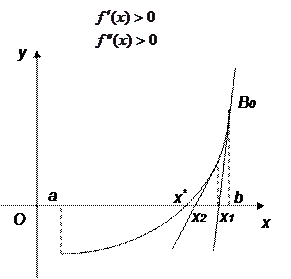

 , т.е.
, т.е.  . Ее уравнение
. Ее уравнение  . Находим x1, полагая y = 0:
. Находим x1, полагая y = 0:  . Корень
. Корень  . Применяя метод еще раз для отрезка
. Применяя метод еще раз для отрезка  , получим
, получим  , где ε; - заданная точность. Тогда xпр = xn+1 с точностью ε;.
, где ε; - заданная точность. Тогда xпр = xn+1 с точностью ε;.


