Этапы приближенного решения нелинейных уравнений.
Приближенное решение уравнения состоит из двух этапов:
Отделение корней можно проводить графически и аналитически. Для того чтобы графически отделить корни уравнения (1), необходимо построить график функции
На практике же бывает удобнее заменить уравнение (1) равносильным ему уравнением
где
Рис 2. Графическое отделение корней (2-ой способ).
Пример 1. Отделить графически корень уравнения Решение. Для решения задачи построим график функции
Рис. 3. График функции
Из рисунка видно, что один из корней уравнения принадлежит отрезку Пример 2. Отделить графически корень уравнения
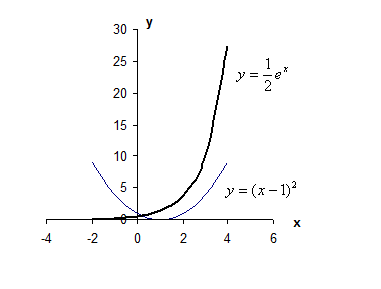
Решение. Преобразуем уравнение к виду  и построим графики функций и построим графики функций  и и 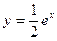 (рис. 4). (рис. 4).
Рис. 4. Графическое отделение корней.
Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку
Аналитическое отделение корней основано на следующих теоремах. Теорема 1. Если непрерывная функция
Рис. 5. Существование корня на отрезке.
Теорема 2. Если непрерывная на отрезке
Рис. 6. Существование единственного корня на отрезке.
Пример 3. Подтвердить аналитически правильность нахождения отрезка изоляции корня уравнения Решение. Для отрезка
Уточнение корней до заданной точности заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Наиболее распространенными являются метод деления отрезка пополам, метод касательных (Ньютона), метод секущих (хорд).
|

 . Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения (рис. 1).
. Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения (рис. 1).
 , (2)
, (2) и
и  - более простые функции, чем
- более простые функции, чем  . Абсциссы точек пересечения графиков функций
. Абсциссы точек пересечения графиков функций 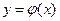 и
и 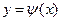 дают корни уравнения (2), а значит и исходного уравнения (1) (рис.2).
дают корни уравнения (2), а значит и исходного уравнения (1) (рис.2).
 .
. (рис. 3).
(рис. 3).
 , второй – отрезку
, второй – отрезку  . Так как рассматриваемое уравнение имеет третью степень, то должен существовать еще один корень на интервале
. Так как рассматриваемое уравнение имеет третью степень, то должен существовать еще один корень на интервале  .
. .
.
 .
. значения разных знаков, т.е.
значения разных знаков, т.е.  , то на этом отрезке содержится по крайней мере один корень уравнения (1) (рис. 5).
, то на этом отрезке содержится по крайней мере один корень уравнения (1) (рис. 5).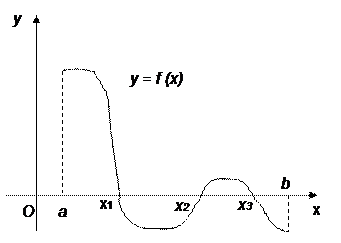
 сохраняет знак внутри отрезка
сохраняет знак внутри отрезка 
 ;
;  Значит,
Значит,  . Следовательно, корень отделён правильно.
. Следовательно, корень отделён правильно.


