Алгоритм приближенного вычисления корня методом хорд.
Исходные данные: f (x) – функция; ε; – требуемая точность; x0 – начальное приближение. Результат: xпр – приближенный корень уравнения f (x) = 0. Метод решения:
Рассмотрим случай, когда  и и 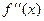 имеют одинаковые знаки (рис. 11). имеют одинаковые знаки (рис. 11).
Рис. 11. Геометрическая интерпретация метода хорд для случая
График функции проходит через точки В аналитической геометрии выводится формула, задающая уравнение прямой, проходящей через две точки с координатами (х1; у1) и (х2; у2): Тогда уравнение хорды А0В0 запишется в виде: Найдем значение х = х1, для которого у = 0: Продолжая этот процесс, находим: В этом случае конец b отрезка Таким образом, получаем расчетные формулы метода хорд:
Вычисления очередных приближений к точному корню уравнения продолжается до тех пор, пока не достигнем заданной точности, т.е. должно выполняться условие: Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е.
Соединим точки Уравнение хорды А0В0: Расчетные формулы метода:
Условие окончания вычислений: Итак, если Практический выбор той или иной формулы осуществляется, пользуясь следующим правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной. Пример 4. Проиллюстрировать действие этого правила на уравнении Решение. Здесь
|


 .
. и
и  . Искомый корень уравнения (точка x*) нам неизвестен, вместо него возьмет точку х1 пересечения хорды А0В0 с осью абсцисс. Это и будет приближенное значение корня.
. Искомый корень уравнения (точка x*) нам неизвестен, вместо него возьмет точку х1 пересечения хорды А0В0 с осью абсцисс. Это и будет приближенное значение корня. .
.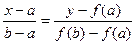 .
. . Теперь корень находится на отрезке
. Теперь корень находится на отрезке  . Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки
. Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки  и
и  .
. . Получаем рекуррентную формулу вычисления приближений к корню
. Получаем рекуррентную формулу вычисления приближений к корню  .
. остается неподвижным, а конец a перемещается.
остается неподвижным, а конец a перемещается. . (4)
. (4) , где
, где  - заданная точность.
- заданная точность. (рис. 12).
(рис. 12).
 . Отсюда найдем
. Отсюда найдем  , полагая y = 0:
, полагая y = 0:  . Теперь корень уравнения
. Теперь корень уравнения  . Применяя метод хорд к этому отрезку, получим
. Применяя метод хорд к этому отрезку, получим  . Продолжая и т.д., получим
. Продолжая и т.д., получим 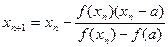 .
.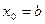 . (5)
. (5) , если отрезок изоляции корня [2;3].
, если отрезок изоляции корня [2;3]. .
. ;
;  . Вторая производная в этом примере положительна на отрезке изоляции корня [2;3]:
. Вторая производная в этом примере положительна на отрезке изоляции корня [2;3]: 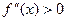 ,
, 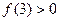 , т.е.
, т.е.  . Таким образом, при решении данного уравнения методом хорд для уточнения корня выбираем формулы (4).
. Таким образом, при решении данного уравнения методом хорд для уточнения корня выбираем формулы (4).


