Лет со дня размещения
Эксплуатация устройства. Сильно загрязненное белье замачивать за 2-3 часа до стирки. Стирку производить в емкости объемом не более 15-20 литров в следующей последовательности: 1. Приготовить емкость для стирки с соотношением ширины дна к высоте не менее чем 1:1,5 (ведро, глубокий таз и т.д.) 2. Наполнить емкость водой температурой 40-50° С для синтетики или 60-65° С для хлопка и льна. Температуру уточнить по ярлыку стираемой ткани. 3. Засыпать в волу стиральный порошок. 4. Опустить на середину емкости излучатель. 5. Погрузить белье (не более 1,5 кг сухою веса). Проследить, чтобы белье свободно плаваю в моющем растворе. Сильно загрязненные места намылить мылом. 6. Подключить устройство в сеть. 7 Время стирки 30-90 минут, в процессе стирки белье переворачивать примерно раз в 10-15 минут. Процесс стирки невидим. Также УСМ эффективно при замачивании белья перед стиркой в обычной машине, при этом эффект дезинфекции также сохраняется. 8. После окончания стирки УСМ отключить от сети, промыть и просушить излучатель. 9. Прополоскать белье. Использование УСМ особенно эффективно при стирке тонких шерстяных вещей тонкого белья и т д. Вещи при этом не перекручиваются не растягиваются и не теряют формы РАДИОАМАТОР 4’2001 Рис. 1.27. Схема к определению распределения скоростей и расхода жидкости при ламинарном движении: а – поток жидкости, движущейся в трубе; б – элементарный слой движущейся жидкости Вследствие действия между слоями сил трения слои будут двигаться с неодинаковыми скоростями. Центральный цилиндрический слой у оси трубы имеет максимальную скорость, но по мере удаления от оси скорость элементарных кольцевых слоев будет уменьшаться. Непосредственно у стенки жидкость как бы «прилипает» к стенке, и ее скорость здесь обращается в нуль.
Выделим в потоке жидкости, ламинарно движущемся по трубе радиусом R (Рис. 1.27, б), цилиндрический слой длиной l и радиусом r. Движение слоя происходит под действием разности сил давления Р1 и P2 с обеих торцовых сторон цилиндра:
где p1, p2 - гидростатические давления в сечениях 1-1 и 2-2. Движению цилиндра оказывает сопротивление сила внутреннего трения Т, для которой справедливо выражение
где ur - скорость движения жидкости вдоль оси цилиндра на расстоянии r от оси; F = Знак минус указывает на убывание скорости с увеличением радиуса r (при r = R величина При установившемся движении разность сил давления P1 - Р2 затрачивается на преодоление силы трения T, и сумма проекций всех этих сил на ось потока должна быть равна нулю. Вследствие трения движение рассматриваемого цилиндрического слоя тормозится, значит, сила трения, приложенная к его боковой поверхности, направлена противоположно разности P1 - Р2 и проектируется на ось, направление которой совпадает с направлением движения, со знаком минус. Следовательно,
откуда, после сокращения и разделения переменных, получим
Переходя ко всему объему жидкости в трубе, проинтегрируем это дифференциальное уравнение, учитывая, что радиус в левой части уравнения изменяется от r до r = R, а переменная скорость в правой части - от u = ur до u = 0 (у стенки, где r = R).
Тогда
Скорость имеет максимальное значение на оси трубы, где r = 0,
Сопоставляя выражения (1.85) и (1.86), находим
Уравнение (1.87) представляет собой закон Стокса, выражающий параболическое распределение скоростей в сечении трубопровода при ламинарном движении. Для определения расхода жидкости при ламинарном движении рассмотрим элементарное кольцевое сечение (см. Рис. 1.27, б) с внутренним радиусом r и внешним радиусом (r + dr), площадь которого равна dS = 2prdr. Объемный расход жидкости через это сечение составляет
или с учетом уравнения (1.85)
Интегрируя последнее уравнение, получим общий расход жидкости через трубу
Подставляя вместо R диаметр трубы d = 2R и обозначая (р1 — р2) = Dр, окончательно находим
Уравнение (1.90) или (1.91), определяющее расход жидкости при ее ламинарном движении по круглой прямой трубе, носит название уравнения Пуазейля. Соотношение между средней скоростью v и максимальной скоростью v max можно получить, сопоставив значение Q из уравнений (1.70) и (1.90),
откуда
Сравнивая уравнения (1.86) и (1.92), находим
Таким образом,при ламинарном потоке в трубе средняя скорость жидкости равна половине скорости по оси трубы. Соответственно параболический закон распределения скоростей по сечению трубы, выражаемый уравнением (1.87), может быть представлен в виде
Уравнение неразрывности (сплошности) потока. Установим общую зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности или неразрывности движения, т. е. не образуется пустот, не заполненных жидкостью.
Тогда, согласно уравнению массового расхода, через эту грань в параллелепипед войдет вдоль оси х за единицу времени масса жидкости r ux dy dz, а за промежуток времени dt - масса жидкости Mx = r ux dy dz dt, (1.95) где r - плотность жидкости на левой грани параллелепипеда. На противоположной (правой) грани параллелепипеда скорость и плотность жидкости могут отличаться от соответствующих величин на левой грани и будут равны Тогда через правую грань параллелепипеда за то же время dt выйдет масса жидкости
Приращение массы жидкости в параллелепипеде вдоль оси x
Если составляющие скорости вдоль осей у и z равны uy и uz, то приращения массы в элементарном объеме вдоль этих осей по аналогии составят
Общее накопление массы жидкости в параллелепипеде за время dt равно сумме ее приращений вдоль всех осей координат:
Вместе с тем изменение массы в полностью заполненном жидкостью объеме параллелепипеда возможно только вследствие изменения плотности жидкости в этом объеме. Поэтому
Приравнивая оба выражения dM, сокращая на (- dx dy dz) и перенося
Уравнение (1.102) представляет собой дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости. Уравнение (1.102) может быть записано и в несколько иной форме. Проводя дифференцирование произведения
или
где В установившемся потоке плотность не изменяется во времени, т. е.
Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока при скоростях, значительно меньших скорости звука, r = const и, следовательно,
Уравнение (1.105) является дифференциальным уравнением неразрывности потока несжимаемой жидкости. Сумма изменений скорости вдоль осей координат в левой части уравнения (1.105) называется дивергенцией вектора скорости и обозначается через div u. Поэтому данное уравнение можно представить как
Для того чтобы перейти от элементарного объема ко всему объему жидкости, движущейся сплошным потоком по трубопроводу переменного сечения (рис. 1.29), проинтегрируем дифференциальное уравнение (1.104). Если бы площадь сечения трубопровода не изменялась, то для установившегося однонаправленного движения (в направлении оси х) интегрирование уравнения (1.104) дало бы зависимость Если же площадь сечения S трубопровода переменна, то, интегрируя также по площади, получим
где Выражение (1.106) или (1.106а) представляет собой уравнение неразрывности (сплошности) потока в его интегральной форме для установившегося движения. Это уравнение называется также уравнением постоянства расхода. Согласно уравнению постоянства расхода, при установившемся движении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одна и та же масса жидкости. Для капельных жидкостей
Следовательно,
где Q = uS - объемный расход жидкости, м3/с. Из уравнения (1.107а) следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений. Согласно уравнению (1.107) массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение постоянства расхода является частным случаем закона сохранения массы и выражает материальный баланс потока. В некоторых случаях, например при вскипании жидкости вследствие резкого понижения давления, образуется пар, что может привести к разрыву потока. В таких условиях, наблюдаемых иногда при работе насосов, уравнение неразрывности потока не выполняется.
лет со дня размещения
|

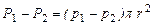 , (1.81)
, (1.81) ,
, - наружная поверхность цилиндра; m - вязкость жидкости.
- наружная поверхность цилиндра; m - вязкость жидкости. = 0).
= 0). или
или  , (1.82)
, (1.82) . (1.83)
. (1.83) . (1.84)
. (1.84) . (1.85)
. (1.85)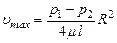 . (1.86)
. (1.86) . (1.87)
. (1.87) , (1.88)
, (1.88)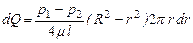 . (1.89)
. (1.89) . (1.90)
. (1.90) . (1.91)
. (1.91) и
и 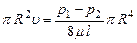 ,
, . (1.92)
. (1.92)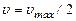 . (1.93)
. (1.93) . (1.94)
. (1.94) Выделим внутри потока элементарный параллелепипед объемом dV = dx dy dz, ребра которого ориентированы параллельно осям координат (Рис. 1.28). Пусть составляющая скорости потока вдоль оси х в точках, лежащих на левой грани параллелепипеда площадью dS = dy dz, равна ux.
Выделим внутри потока элементарный параллелепипед объемом dV = dx dy dz, ребра которого ориентированы параллельно осям координат (Рис. 1.28). Пусть составляющая скорости потока вдоль оси х в точках, лежащих на левой грани параллелепипеда площадью dS = dy dz, равна ux.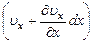 и
и 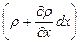 .
. . (1.96)
. (1.96) . (1.97)
. (1.97)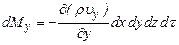 , (1.98)
, (1.98) . (1.99)
. (1.99) . (1.100)
. (1.100) . (1.101)
. (1.101) в левую часть уравнения, окончательно получим
в левую часть уравнения, окончательно получим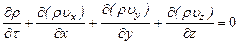 . (1.102)
. (1.102) , получим
, получим
 , (1.103)
, (1.103)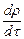 - субстанциональная производная плотности.
- субстанциональная производная плотности. . (1.104)
. (1.104) . (1.105)
. (1.105) . (1.105a)
. (1.105a) const, где u - средняя скорость жидкости.
const, где u - средняя скорость жидкости. const. (1.106)
const. (1.106) Для трех различных сечений (1-1, 2-2 и 3-3) трубопровода, изображенного на Рис. 1.29, имеем
Для трех различных сечений (1-1, 2-2 и 3-3) трубопровода, изображенного на Рис. 1.29, имеем , или
, или 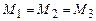 , (1.106a)
, (1.106a) - массовый расход жидкости, кг/с.
- массовый расход жидкости, кг/с. const, и уравнение (1.106) принимает вид
const, и уравнение (1.106) принимает вид const. (1.107)
const. (1.107)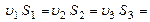 const или
const или  , (1.107a)
, (1.107a)


