Практическая работа № 3
В практике корректирование профиля фасонного резца производят аналитическим методом, обеспечивающим высокую точность. Для нахождения размеров резца с точностью до 0,01 мм расчет линейных размеров ведут с точностью до 0,001 мм и до 1011 для угловых размеров с последующим округлением до 0,01 мм или 1°. Обозначим цифрами 1,2..8 узловые точки заданного профиля. Радиусы r1, r2..r8 до узловых точек детали найдены выше. Для расчета профиля круглых фасонных резцов необходимо определить расстояние Сi1 по передней грани от 1-ой точки до точки 8.
Искомые координатные расстояния глубины профиля
где
Федеральное агентство по образованию. Государственное образовательное учреждение Высшего профессионального образования. Нижегородский государственный университет Имени Н.И. Лобачевского Факультет подготовки региональных кадров Специальность «Таможенное дело» Практическая работа № 3 Дисциплина: «Информационные таможенные системы» Тема: «Исследование биноминального и нормального распределения случайных величин с помощью табличного процессора Excel»
Выполнил: студент 4 курса, очной формы обучения, группа № 2-14ТД/13, Фролов А.С. _______________ подпись Научный руководитель:В.А. Гришин
_______________ подпись
г. Нижний Новгород 2013г.
Содержание
Цель
1. Теоретические сведения
2. Ход выполнения практической работы
Заключение. Выводы.
Список литературы
Цель. Целью данной практической работы является: 1. Исследование биноминального и нормального распределения случайных величин с помощью табличного процессора Excel; 2. Генерация случайных чисел функциями Excel.
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. БИНОМИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ: Дискретная случайная величина Х распределена по биноминальному распределению, если она принимает значение 0,1,2,3,…..n с вероятностями Pm,n = C n = Где р – вероятность успеха N – Число независимых испытаний M – Число успехов MX = n*p, DX = n*p*(1-p) Примером практического использования биноминального распределения может являться угадывание правильных ответов при контроле занятий студентов тестами закрытого типа. Функция использует следующие параметры: БИНОМРАСП (ЧИСЛО УСПЕХОВ; ЧИСЛО ИСПЫТАНИЙ; ВЕРОЯТНОСТЬ УСПЕХА; ИНТЕГРАЛЬНАЯ) Число успехов – количество успешных испытаний Число испытаний – число независимых испытаний Вероятность успеха – вероятность успеха каждого испытания Интегральный – логическое значение, определяющее форму функций. Если данный параметр имеет значение истина (=1), то считается интегральная функция распределения (вероятность того, что число успешных испытаний не менее значения число успехов); Если этот параметр имеет значение ложь (=0), то вычисляется значение функции плотности распределения (вероятность того, что число успешных испытаний в точности равно значению аргумента число успехов). НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ: Нормальный закон (закон Гаусса) играет исключительную роль в теории вероятностей и статистике. Главная особенность закона состоит в том, что он является придельным законом к которому приближаются, при определенных условиях, другие законы распределения. Нормальный закон наиболее часто встречается в практике. Непрерывная случайная величина Х распределена по нормальному распределению с параметрами, если ее плотность распределения имеет вид
M - Среднее арифметическое значение Х - среднее квадратическое отклонение. В Excel для вычислений значений нормального распределения используется функции НОРМРАСП, которая вычисляет значение вероятностей функции распределения для указанного среднего и стандартного отклонения. Функция имеет параметры: НОРМРАСП (Х; СРЕДНЕЕ; СТАНДАРТНОЕ ОТКЛОНЕНИЕ; ИНТЕГРАЛЬНАЯ) Х – значение выборки, для которых строится распределение Среднее – среднее арифметическое выборки Стандартное отклонение –стандартное отклонение распределения Интегральный – логическое значение, определяющее форму функции. Если интегральная имеет значение истина (1), то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности распределения. Если среднее =0 и стандартное откл = 1 то функция НОРМРАСП возвращает стандартное нормальное распределение.
ГЕНЕРАЦИЯ СЛУЧАЙНЫХ ВЕЛИЧИН: Еще одним аспектом использование законов распределения вероятностей является генерация случайных величин. Бывают ситуации, когда необходимо получить последовательность случайных чисел. Это в частности требуется для моделировании объектов имеющих случайную природу по известному распределению вероятностей. Процедура генерации случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из одного или нескольких распределений. В MS Excel для генерации СВ используются функции из категории математические: СЛЧИС – выводит на экран равномерно распределенные случайные числа больше или равные 0 и меньше 1; СЛУЧМЕЖДУ – выводит на экран случайное число, лежащие между произвольными заданные значениями. В случае использование процедуры генерация случайных чисел из пакета анализа необходимо заполнить следующие поля: - число переменных вводится число столбцов значений которые необходимо разместить в выходном диапазоне. Если это число не введено, то все столбцы в выходном диапазоне будут заполнены; - число случайных чисел вводится число случайных значений, которое необходимо вывести для каждой переменной, если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены; - в поле распределение необходимо выбрать тип распределения, которое следует использовать для генерации случайных переменных: 1. равномерное – характеризуется верхними и нижними границами. Переменные извлекаются с одной и той же вероятностью для все значений интервала. 2. нормальное – характеризуется средним значением и стандартным отклонением. Обычно для этого распределения используют среднее значение 0 и стандартное отклонение 1. 3. биноминальное – характеризуется вероятностью успеха для некоторого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биноминальной случайной переменной; 4. дискретное – характеризуется значением СВ и соответствующем ему интервалом вероятностей, диапазон должен состоять из двух столбцов: левого, содержащего значения, и правого, содержащего вероятности связанные со значением в данной строке. Сумма вероятностей должна быть равна 1; 5. распределение Бернулли Пуассона и Модельное - в поле случайное рассеивание вводится произвольное значение для которого необходимо генерировать случайные числа. Впоследствии можно снова использовать это значение для получения тех же самых случайных чисел. - выходной диапазон вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае наложения выходного диапазона на исходные данные.
|


 – радиусы базовой 1 и i-ой узловой точки соответственно.
– радиусы базовой 1 и i-ой узловой точки соответственно.





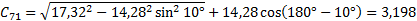

 в осевом сечении круглого фасонного резца для наружной обработки могут быть вычислены по формулам
в осевом сечении круглого фасонного резца для наружной обработки могут быть вычислены по формулам

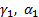 – передний и задний углы для базовой точки 1
– передний и задний углы для базовой точки 1 – радиус резца
– радиус резца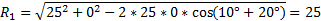







 , мм
, мм
 , мм
, мм
 , мм
, мм
 , мм
, мм
 , мм
, мм
 , мм
, мм
 , мм
, мм
 , мм
, мм
 , мм
, мм
 , мм
, мм
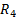 , мм
, мм
 , мм
, мм
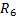 , мм
, мм
 , мм
, мм
 , мм
, мм
 -
- -
-


