Ход выполнения практической работы.

Пример 1: Какова вероятность того, что при ответе на 35 вопросов теста с четырьмя вариантами ответов студент угадает 9 верных ответов?

Решение:

1. Устанавливаем табличный курсор в свободную ячейку, например в А1.значение искомой вероятности.

2. Для получения значения вероятности воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка функции (fx).

3. В появившимся диалоговом окне Мастер функции – шаг 1 из 2 слева в поле Категория указаны виды функции. Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП и нажимаем на кнопку ОК.

В поле число вводим 9 количество успешных испытаний. В поле испытания вводим общее количество испытаний 35. В рабочее поле вероятность вводим вероятность успеха в отдельном испытании 0,25.в поле интегральный вводим вид функции распределения- интегральная или весовая 0. И нажимаем кнопку ОК.

В ячейке появляется искомое значение вероятности р= 0,152.

0,152020975

0,626324

 

Задание

1. Построить ряд и многоугольник распределения числа угаданных студентом верных ответов на 35 вопросов закрытого типа с четырьмя вариантами ответов

 

Число верно угаданных ответов			…
Вероятность Pm,n

 

Пример 2

Построить график нормальной функции распределения f(x) при х, меняющемся от 19,8 до 28,8 с шагом 0,5, m = 24,3 = 1,5

Решение

1. В ячейку А1 вводим символ случайной величины х, а в ячеку В1 – символ функции плотности вероятности – f(x).

2. Вводим в диапозон А1:А2 значения ч от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся маркером автозаполнения в ячейку А2 вводим левую границу диапозона 19,8 в ячейку А3 левую границу плюс шаг 20,3. Выделяем блок А2:А3. Затем за правый нижний угол протягиваем мышью до ячейки А21.

3. Устанавливаем табличный курсор в ячейку В2 и для получения значения вероятности пользуемся специальной функцией – нажимаем на панели инструментов кнопку Вставка функции (fx). В появившимся диалоговом окне Мастер функции – шаг 1 из 2 слева в поле Категория указаны виды функции. Выбираем статистическая. Справа в поле функция выбираем функцию НОРМРАСП. Нажимаем ОК.

4. Появляется диалоговое окно НОРМРАСП

В рабочее поле Х вводим адрес ячейки А2 щелчком мыши на этой ячейки. В рабочее поле среднее вводим значение математического ожидания 24,3. В рабочее поле стиандартное откл вводим значение среднеквадратического отклонения 1,5.в рабочее поле интегральное вводим вид функции распределения 0. Нажимаем кнопку ОК.

5. В ячейке В2 появляется вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного курсора протягиванием из ячейки В2 до В21 копируем функцию НОРМРАСП в диапозон В3:В21.

6. По полученным данным строим искомую диаграмму нормальной функции распределения.

Задание

Построить функцию плотности вероятности нормального распределения f(x) при х меняющемся от 0 до 35 с шагом 1 и исследовать ее поведение при постоянном значении среднего арифметического m = 17,5 и трех значениях = 2, = 4, = 6. Постоянном значении = 2 и трех значениях m = 8. m = 17. m=26

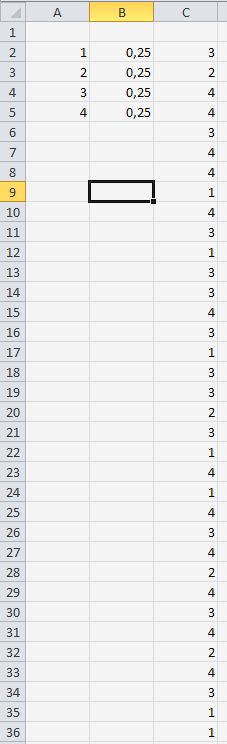
Пример 3

Констатируется текст закрытого типа. В тест входит 35 вопросов. Каждый вопрос имеет четыре варианта ответа и один из них верный. Необходимо установить порядок следования верных ответов в вопросах теста, так чтобы они следовали случайно.

Решение

1. Прономеруем ответы по порядку 1,2,3,4. Введем числа от 1-4 в диапазон А2:А5 рабочей таблицы.

2. Укажем желаемую вероятность появления каждого ответа. Пусть все ответы будут равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.

3. Выбираем анализ данных и далее указываем строку генерация случайных величин

В появившимся диалоговом окне указываем число переменных – 1, число случайных чисел – 35 (количесто вопросов тесте). В поле распределение указываем дискретное(только натуральные числа). В поле выходной интервал значений и вероятностей вводим диапазон, содержащие номера вероятности – А2:В5.

4. Указываем выходной диапазон и нажимаем ОК. в столбце С появляются случайные числа 1,2,3,4.

 

Задание

1.сформировать выборку из 10 случайных величин лежащих в диапазоне от0 до 1.

2. сформировать выборку из 20 случайных величин лежащих в диапазоне от 5 до 20.

3. составить расписание на месяц для случайной демонстрации на телевидении одного из четырех рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1 должна быть в два раза выше чем остальных рекламных роликов.

 

ЗАКЛЮЧЕНИЕ.

При выполнении практической работы получены следующие результаты:

Изучили законы распределения случайных величин и генерацию случайных чисел.

 

 

СПИСОК ЛИТЕРАТУРЫ.

1. Вуколов «Компьютерный анализ статистических данных» 2012г.

2. Лекция

3. Теоретический материал из практической работы.

4. Мидитон «Анализ статистических данных с использованием EXL» 2005г.

5. Афонин П.Н. «ИТТ» 2012г.

6. Программа Excel