Некоторые дискретные распределения
Распределение Пуассона Ряд распределения: Функция распределения: Применение в биологии: Поведение биологических объектов, соответствующее закону Пуассона, наблюдается в том случае, когда по пробам случайно распределены редкие объекты. Примеры: число лейкоцитов, наблюдаемых в одном квадрате гемоцитометра, частота нарушений хромосомного аппарата на каждую тысячу митозов, встречаемость семян сорняка в большой серии навесок семян культурного растения, число повторных попаданий животных в ловушки, отловы животных в отдельные промежутки времени при длительных наблюдениях, встречаемость животных на отрезках длинных маршрутов или на пробных площадках обширной территории. Биномиальное распределение Ряд распределения: Функция распределения: Применение в биологии: Примерами описания признаков с помощью биномиального распределения могут служить: число больных корнеплодов в пробе, число поврежденных участков на листьях, число волосков на единице площади шкурки, количество лучей в плавниках рыб, число хвостовых щитков у рептилий, плодовитость (размер выводка) самок и т.п. В основе биномиального распределения лежит альтернативное проявление изучаемого признака: он может присутствовать или отсутствовать у единичного объекта, проявиться или нет. Например, если имеется n индивидуумов и вероятность того, что какой-либо из них обладает определенным признаком, равна p (независимо от других индивидуумов), то вероятность наблюдения r индивидуумов с данным признаком равна:
Распределение Пойа Ряд распределения:
где x = 1, 2, …, n – 1;
где n > 0, b > 0, r > 0, c – целые числа. Параметр c может быть отрицательным, но должен удовлетворять условию b + r + c (n – 1) > 0. Применение в биологии: моделирование эпидемий инфекционных заболеваний.
|

 , где x = 0, 1, 2, …; µ – математическое ожидание (µ > 0).
, где x = 0, 1, 2, …; µ – математическое ожидание (µ > 0).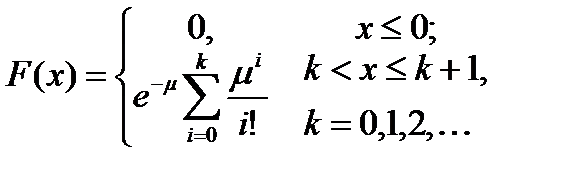
 , где x = 0, 1, 2, …, n;
, где x = 0, 1, 2, …, n;  – целое число, 0 < p < 1, q = 1 – p;
– целое число, 0 < p < 1, q = 1 – p;  – биномиальный коэффициент (число сочетаний из n элементов по x).
– биномиальный коэффициент (число сочетаний из n элементов по x).
 , где
, где 
 ;
; ,
, ,
,


