Некоторые непрерывные распределения
Нормальное распределение Плотность вероятности: Применение в биологии: большинство мерных признаков распределены по закону нормального распределения.
Логнормальное распределение Плотность вероятности: Применение в биологии: распределение видов в сообществах.
Распределение Максвелла Плотность вероятности: Применение в биологии: описание расщепления особей в популяции по определенному признаку.
Распределение Шарлье Плотность вероятности: Применение в биологии: описание распределения мерных признаков, например, длины хвои у сосны обыкновенной.
Рассмотрим простейшую стохастическую модель роста популяции на основе детерминистической модели экспоненциального роста. Напомним, что в детерминистической модели численность популяции N за время dt увеличивается на
Подойдем к процессу роста популяции с вероятностной точки зрения. Пусть вероятность появления одного потомка у данной особи в интервале времени dt равна rdt, тогда вероятность появления одной новой особи в целой популяции за это же время равна Nrdt. Соответственно вероятность непоявления одного потомка у данной особи в интервале времени dt равна (1 – rdt), а вероятность непоявления одной новой особи в целой популяции за это же время равна 1 – Nrdt. Мы имеем дело с двумя альтернативными состояниями одного признака. Сумма вероятности появления и вероятности непоявления потомка равна единице. Обозначим через PN (t) вероятность того, что в момент t в популяции имеется ровно N особей. Предположим, что в каждый момент времени может произойти только одно из двух событий: за время dt численность популяции может увеличиться на 1, либо остаться неизменной. Свяжем размер популяции в момент времени t с размером популяции в момент t + dt. Если число особей в момент t + dt равно N, это означает, что либо их было N – 1 в момент времени t и за интервал dt появилась еще одна особь, либо в момент времени t их было N и численность популяции не менялась. Складывая вероятности, получим: PN (t + dt) = PN – 1 (t) r (N – 1) dt + PN (t)(1 – Nrdt) Преобразуем это выражение:
Это уравнение справедливо при N > N 0. При N = N 0 отсутствует член, содержащий
Проинтегрируем последнее уравнение с учетом того, что
Подставляем полученный результат в уравнение для N 1 = N 0 + 1. Используем начальное условие
Введем дополнительную функцию (μ(t)), равную:
Умножим левую и правую части предыдущего выражения на эту функцию:
С учетом того, что:
Получаем:
На основе следующего выражения (см. курс дифференциальных уравнений):
Получим:
Проинтегрируем обе части выражения по t:
Поскольку C 1 = 0 (
Таким же способом рассчитаем вероятность для N 2, N 3. После этого можно определить вероятность для NN (табл. 1). Таблица 1
Математическое ожидание равно:
Рассмотрим стохастическую модель, которая позволяет теоретически оценить вероятность достижения растительностью климаксового состояния. Согласно Уиттекеру можно выделить пять типов климаксов в зависимости от их устойчивости, которая рассматривается как функция двух основных показателей: времени генерации доминантов (Z) и продолжительности циклов резких изменений условий среды (X). Первые два типа климакса (аклимакс и циклоклимакс) собственно климаксами не являются (для аклимакса Z > X флуктуации сообщества беспрестанны, серийные и климаксовые сообщества неразличимы, например фитопланктон; для циклоклимакса Z ≈ X, например сообщества однолетников в пустыне). Три остальных типа (катаклимакс, суперклимакс и эуклимакс; Z < X) представляют определенные ступени развития фитоценозов на пути к устойчивому состоянию. Эти типы различаются биомассой сообществ и степенью отличия климаксовых сообществ от серийных. На Z и X оказывает воздействие большое число различных причин, что позволяет рассматривать их как случайные величины. Таким образом, можно считать, что растительность достигает климаксового состояния, если осуществляется событие Z < X, т.е. время развития доминанта будет меньше, чем время между двумя резкими изменениями среды, которые могут его погубить. Так как Z и X – случайные величины, то событие Z < X либо произойдет в каждой конкретной ситуации, либо нет. Будем интересоваться вероятностью (P) осуществления события Z < X на интервале времени [0, t ], которое запишется следующим образом (Розенберг, 1984):
где FX (τ) и FZ (τ) – функции распределения случайных величин X и Z. Данный тип вероятности получил название вероятность «успеть подготовиться к катастрофе» и детально изучен С.Ю. Рудерманом (1963, 1965). В каждой конкретной ситуации могут быть выбраны определенные законы распределения FX и FZ и оценены их параметры. Так, в качестве закона распределения для времени между случайными и резкими изменениями среды, например, пожарами или ветровалами можно использовать закон распределения Вейбулла. Для времени генерации доминантов предложен более сложный закон распределения – закон Вальда, который тесно связан с логарифмически нормальным распределением (считается, что фитомасса домананта распределена логарифмически нормально и его генерация происходит, если эта биомасса B(τ) превысит некоторый заданный порог B0) (Розенберг, 1984). Для больших значений τ имеет место следующая приближенная оценка закона распределения Вальда (Башаринов, Флейшман, 1962):
где d и τ; – параметры распределения, выражающиеся через ln B 0 и математическое ожидание и дисперсию случайных коэффициентов пропорциональности прироста фитомассы доминирующего вида за единицу времени (по предположению подчиняющихся логарифмически нормальному распределению). Таким образом, при достаточно общих предположениях о динамике вида вероятность достижения им устойчивого состояния с учетом распределения Вейбулла и Вальда имеет следующий вид:
где τ0, θ и α – параметры распределения Вейбулла. Несмотря на ужасный вид этого выражения, вычисления по данной формуле сравнительно просты – функция распределения Вальда табулирована. Еще более простую запись вероятности Pt (Z < X) можно получить, предположив нормальность законов распределения Z и X.
|

 , где σ > 0 – параметр масштаба (стандартное отклонение) и µ – параметр положения (математическое ожидание).
, где σ > 0 – параметр масштаба (стандартное отклонение) и µ – параметр положения (математическое ожидание). , где a – параметр формы, m – параметр масштаба (медиана).
, где a – параметр формы, m – параметр масштаба (медиана). , где a – параметр масштаба.
, где a – параметр масштаба. , где µ – параметр положения, математическое ожидание; σ; – параметр масштаба, стандартное отклонение; γ1 – параметр формы асимметрия, γ2 – параметр формы, эксцесс; φ;(x) – плотность вероятности стандартного нормального распределения; φ;(s)(x) – s -я производная плотности вероятности φ;(x) стандартного нормального распределения (s = 3, 4).
, где µ – параметр положения, математическое ожидание; σ; – параметр масштаба, стандартное отклонение; γ1 – параметр формы асимметрия, γ2 – параметр формы, эксцесс; φ;(x) – плотность вероятности стандартного нормального распределения; φ;(s)(x) – s -я производная плотности вероятности φ;(x) стандартного нормального распределения (s = 3, 4). , где r – скорость роста популяции, а N 0 – начальная численность популяции, тогда:
, где r – скорость роста популяции, а N 0 – начальная численность популяции, тогда:
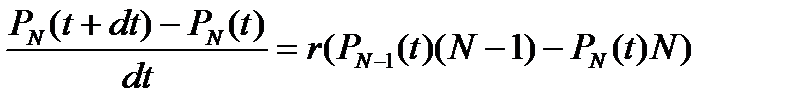 ,
, ,
, :
: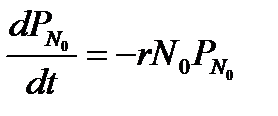
 . Получим:
. Получим: ,
, ,
, ,
, ,
,
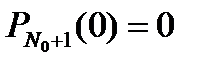 . Получим:
. Получим:
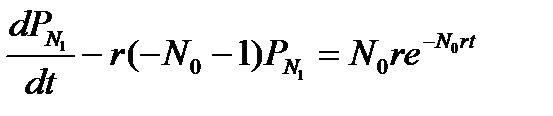

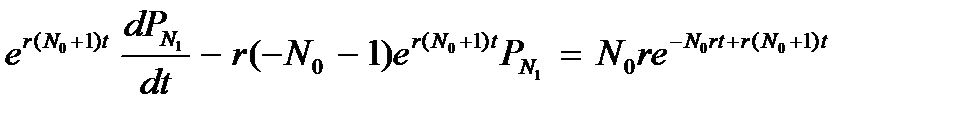





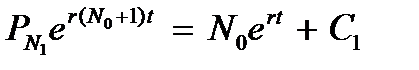

 ):
):
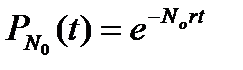



 , для NN > N0
, для NN > N0
 , где
, где 


 ,
, ,
,


