Передача энергии по симметричной цепи с учётом потерь
Тема 5. Теория направляющих систем
При передаче энергии по НС потери в проводнике определяются радиальной составляющей вектора Пойтинга, которую формирует составляющие
откуда где L – внутренняя индуктивность проводника, а R - его активное сопротивление. Анализируем гармонические колебания в квазистационарном режиме, среда не содержит сторонних токов, токи смещения отсутствуют, т.е. Для определения составляющих поля необходимо воспользоваться уравнениями Максвелла:
Применим операцию
Для любого вектора
где Решение уравнений Максвелла для цилиндрического проводника целесообразно проводить в цилиндрической системе координат. Тогда
Учитывая отсутствие в системе сторонних токов, а следовательно и свободных зарядов, Тогда (5.4) с учётом (5.3) примет вид:
Полученное уравнение называется волновым. Обычно волновое уравнение решается для продольных составляющих поля Распределение продольных составляющих поля вдоль линии представляется как
где
Это выражение описывает структуру поля в поперечном сечении системы. Первый сомножитель определяет распределение поля в радиальном направлении, второй в азимутальном. где A, B, C, D – постоянные интегрирования, Так как поле внутри проводника возрастает от центра к периферии, а функция
Составляющую магнитного поля определим как
и аргумент этих функции имеет вид т. к. Таким образом, полученные выражения
где I – ток в цепи. Далее необходимо в (6.12) подставить (6.9) и (6.10) и (6.11), произвести соответствующие преобразования. Дальнейшие преобразования являются достаточно громадно, окончательные выражения для активного сопротивления и внутренней индуктивности принимают вид
Внутренняя индуктивность симметричной цепи определяется выражением, Гн/км где d – диаметр проводника, а – расстояние между ними (рис. 5.1), С учётом различных скруток в кабеле выражение для расчёта сопротивления симметричного кабеля имеет вид, Ом/км
При парной скрутке
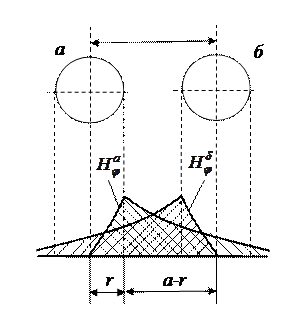
Рис. 5.1 – Поле симметричной пары
Первое слагаемое в (5.15) определяет сопротивление цепи по постоянному току, второе – сопротивление вследствие поверхностного эффекта, а третье – сопротивление вследствие эффекта близости.
|

 и
и 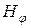 .Мощность потока энергия для цилиндрического проводника определяется
.Мощность потока энергия для цилиндрического проводника определяется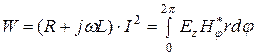 ,
, , (5.1)
, (5.1)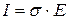 .
.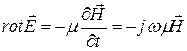 ; (5.2)
; (5.2)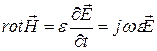 . (5.3)
. (5.3)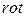 к (4.2):
к (4.2): . (5.4)
. (5.4)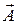 выполняется тождество
выполняется тождество , (5.5)
, (5.5)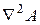 - оператор Лапласа.
- оператор Лапласа. .
.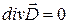 и
и 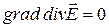 .
.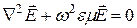 . (5.6)
. (5.6)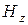 , которые дают возможность определить все шесть составляющих электромагнитного поля.
, которые дают возможность определить все шесть составляющих электромагнитного поля.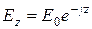 . Тогда волновое уравнение примет вид
. Тогда волновое уравнение примет вид , (5.7)
, (5.7) - поперечное волновое число, для Т – волн
- поперечное волновое число, для Т – волн 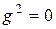 , т.е.
, т.е. 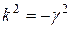 , т.к. анализируется процесс распространения в металле, обозначим
, т.к. анализируется процесс распространения в металле, обозначим  - волновое число для металла. Уравнение (5.7) – это уравнение частных в производных с разделяющимися переменными, его решение для металла имеет вид:
- волновое число для металла. Уравнение (5.7) – это уравнение частных в производных с разделяющимися переменными, его решение для металла имеет вид: , (5.8)
, (5.8)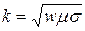 - коэффициент вихревых токов для металла,
- коэффициент вихревых токов для металла,  и
и 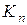 - модифицированные функции Бесселя n –го порядка второго рода. Постоянные интегрирования определяются из граничных условий на границе раздела сред металл / диэлектрик.
- модифицированные функции Бесселя n –го порядка второго рода. Постоянные интегрирования определяются из граничных условий на границе раздела сред металл / диэлектрик. . В силу симметричного расположения проводников относительно горизонтальной оси, нечётная функция
. В силу симметричного расположения проводников относительно горизонтальной оси, нечётная функция 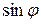 должна обращаться в нуль, т.е.
должна обращаться в нуль, т.е.  . Учитывая наличие бесконечного числа составляющих поля, получим
. Учитывая наличие бесконечного числа составляющих поля, получим  . (5.9)
. (5.9)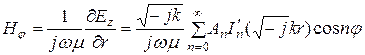 . (5.10)
. (5.10)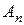 определяются из граничных условий и закона полного тока. Функции Бесселя второго рода это функции комплексной переменной, представляются в виде суммы действительной и мнимой составляющих.
определяются из граничных условий и закона полного тока. Функции Бесселя второго рода это функции комплексной переменной, представляются в виде суммы действительной и мнимой составляющих.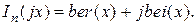 (5.11)
(5.11) .
. . (5.12)
. (5.12)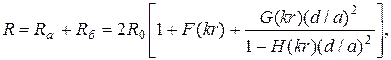 (5.13)
(5.13)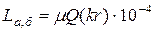 , (5.14)
, (5.14)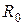 - сопротивление проводника по постоянному току. Функции I, F, H, G, Q определяются комбинациями функций Бесселя, их значения приведены в таблицах (см. приложение),
- сопротивление проводника по постоянному току. Функции I, F, H, G, Q определяются комбинациями функций Бесселя, их значения приведены в таблицах (см. приложение), 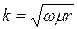 , r– радиус проводника.
, r– радиус проводника.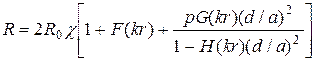 . (5.15)
. (5.15)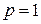 , при звёздной –
, при звёздной – 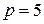 , при двойной парной -
, при двойной парной - 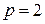 ;
; 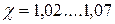 в зависимости от диаметра кабеля. На рис. 5.1 приведено распределение магнитного поля симметричной пары. Поля проводников а и б взаимодействуя между собой увеличивают сопротивление цепи.
в зависимости от диаметра кабеля. На рис. 5.1 приведено распределение магнитного поля симметричной пары. Поля проводников а и б взаимодействуя между собой увеличивают сопротивление цепи.