- Если
 — линейное нормированное пространство и последовательности отображений
— линейное нормированное пространство и последовательности отображений  и
и 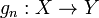 ,
, 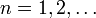 равномерно сходятся на множестве
равномерно сходятся на множестве  , то последовательности
, то последовательности  также как и
также как и  при любых
при любых 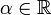 также равномерно сходятся на
также равномерно сходятся на  .
.
- Для вещественнозначных функций (или, более обще, если
 — линейное нормированное кольцо), последовательность отображений
— линейное нормированное кольцо), последовательность отображений 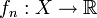 , равномерно сходится на множестве
, равномерно сходится на множестве  и
и  ограниченное отображение, то последовательность
ограниченное отображение, то последовательность  также равномерно сходится на
также равномерно сходится на  .
.
- Если
 — топологическое пространство,
— топологическое пространство,  — метрическое пространство и последовательность непрерывных в точке
— метрическое пространство и последовательность непрерывных в точке  отображений
отображений  равномерно сходится на множестве
равномерно сходится на множестве  к отображению
к отображению  , то это отображение также непрерывно в точке
, то это отображение также непрерывно в точке 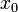 .
.
- Если последовательность интегрируемых по Риману (по Лебегу) функций
 равномерно сходится на отрезке
равномерно сходится на отрезке  к функции
к функции  , то эта функция также интегрируема по Риману (соответственно по Лебегу), и для любого
, то эта функция также интегрируема по Риману (соответственно по Лебегу), и для любого  имеет место равенство
имеет место равенство

и сходимость последовательности функций

на отрезке  к функции
к функции
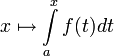
равномерна.
- Если последовательность непрерывно дифференцируемых на отрезке
 функций
функций  , сходится в некоторой точке
, сходится в некоторой точке 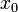 , a последовательность их производных равномерно сходится на
, a последовательность их производных равномерно сходится на  , то последовательность
, то последовательность  также равномерно сходится на
также равномерно сходится на  , её предел является непрерывно дифференцируемой на этом отрезке функцией.
, её предел является непрерывно дифференцируемой на этом отрезке функцией.
· ВЕЙЕРШТРАССА ПРИЗНАК
· равномерной сходимости - утверждение, дающее достаточные условия равномерной сходимости ряда или последовательности функций посредством сравнения их с соответствующими числовыми рядами и последовательностями; установлен К. Вейерштрассом [1]. Если для ряда
· 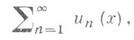
· составленного из действительных или комплексных функций, определенных на нек-ром множестве Е, существует числовой сходящийся ряд
· 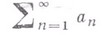
· такой, что
· 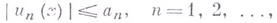
· то исходный ряд сходится равномерно и абсолютно на множестве Е. Напр., ряд
· 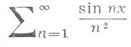
· абсолютно сходится на всей действительной оси, поскольку
· 
· и ряд
·  t
t
· СХОДИТСЯ.
· Если для последовательности действительных или комплексных функций  сходящейся на множестве
сходящейся на множестве  к функции
к функции  , существует бесконечно малая числовая последовательность
, существует бесконечно малая числовая последовательность  такая, что
такая, что  то данная последовательность сходится на множестве Еравномерно. Напр., последовательность
то данная последовательность сходится на множестве Еравномерно. Напр., последовательность
·

· равномерно на всей действительной оси сходится к функции 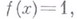 так как
так как
· 
· В. п. равномерной сходимости переносится на функции, значения к-рых лежат в нормированных линейных пространствах.

 — линейное нормированное пространство и последовательности отображений
— линейное нормированное пространство и последовательности отображений  и
и 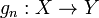 ,
, 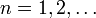 равномерно сходятся на множестве
равномерно сходятся на множестве  , то последовательности
, то последовательности  также как и
также как и  при любых
при любых 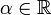 также равномерно сходятся на
также равномерно сходятся на 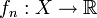 , равномерно сходится на множестве
, равномерно сходится на множестве  ограниченное отображение, то последовательность
ограниченное отображение, то последовательность  также равномерно сходится на
также равномерно сходится на  отображений
отображений  , то это отображение также непрерывно в точке
, то это отображение также непрерывно в точке 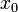 .
. равномерно сходится на отрезке
равномерно сходится на отрезке  к функции
к функции  , то эта функция также интегрируема по Риману (соответственно по Лебегу), и для любого
, то эта функция также интегрируема по Риману (соответственно по Лебегу), и для любого  имеет место равенство
имеет место равенство

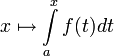
 также равномерно сходится на
также равномерно сходится на 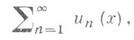
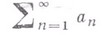
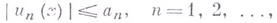
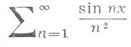

 t
t сходящейся на множестве
сходящейся на множестве  к функции
к функции  , существует бесконечно малая числовая последовательность
, существует бесконечно малая числовая последовательность  такая, что
такая, что  то данная последовательность сходится на множестве Еравномерно. Напр., последовательность
то данная последовательность сходится на множестве Еравномерно. Напр., последовательность
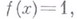 так как
так как



