Гипотеза Бернштейна
В 1905 г Бернштейн выдвинул гипотезу возникновения мембранного потенциала в покое. Он утверждал, что разность потенциалов на мембране обусловлена: 1. наличием разности концентраций ионов К+ и Na+ в цитоплазме клетки и снаружи. 2. В покое мембрана проницаема только для ионов К+.
В связи с этим был выведен равновесный калиевый потенциал, который определяется из уравнения Нернста
или
Исходя из гипотезы Бернштейна для мышечных волокон мембранный потенциал равен (-110) мВ, а экспериментальные данные давали (-90) мВ. Причина в расхождении в том, что гипотеза Бернштейна не учитывала проницаемость мембраны для других ионов, таких как Na+ и Cl-. Поэтому, уравнение Нернста для расчёта мембранного потенциала в покое не подходит. Соответственно, использовали уравнение Гольдмана-Ходжкина-Катца:
В покое проницаемость мембраны для различных ионов будет составлять:
Потенциал действия - изменение мембранного потенциала между внутренней и внешней поверхностью мембраны при возбуждении. Потенциал действия так же зарегистрировали с помощью микроэлектродной техники.
На экране осциллографа было видно (Рис.6), что возбуждающий импульс вызывает смещение мембранного потенциала - φ лишь на короткое время - t, после которого снова восстанавливается мембранный потенциала покоя. 1 - фаза деполяризации, во время которой ионы Na+ большим потоком поступают (затекают) в клетку по градиенту электрохимического потенциала (grad Так же 3 - фаза гиперполирязации связана с остточным калием через мембрану наружу. Новый потенциал действия может сформироваться только после полного возвращения мембраны в состояние покоя. Длительность потенциала действия для нервных волокон и скелетных мышц составляет примерно 1мс, а для миокарда ≈ 300 мс. При возбуждении проницаемость мембраны для различных ионов будет составлять:
Свойства потенциала действия: 1. Наличие порогового значения деполяризующего потенциала; 2. Закон называется «всё или ничего» т.е если деполяризующий потенциал развивается и достигает порогового значения (что зависит от концентрации Na) то он развивается и дальше. 3. Наличие периода рефрактерности т.е невозбудимости мембраны во время развития потенциала действия и остаточных явлений после снятия возбуждения; 4. При возбуждении резко уменьшается сопротивление мембраны.
Амплитуда потенциала действия зависит от концентрации ионов Na снаружи. Если концентрация ионов Na будет уменьшаться снаружи, то и амплитуда потенциала действия тоже будет уменьшаться. Если полностью удалить ионы Na из окружающей клетку среды, то потенциал действия развиваться не будет.
Возбуждение мембраны описывается уравнением Ходжкиным-Хаксли
где
|



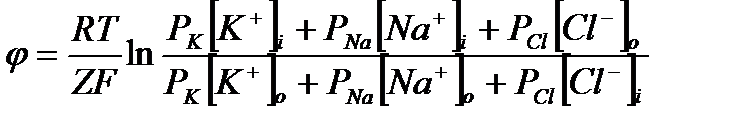
 . Т.е можно сказать, что наибольший вклад в значение мембранного потенциала φ вносят ионы К+.
. Т.е можно сказать, что наибольший вклад в значение мембранного потенциала φ вносят ионы К+.
 При этом первый и второй электроды помещали в аксон. На первый электрод - 1 подаётся электрический импульс с генератора, а с помощью второго электрода -2 измеряли мембранный потенциала высокоумным регистратором напряжения.
При этом первый и второй электроды помещали в аксон. На первый электрод - 1 подаётся электрический импульс с генератора, а с помощью второго электрода -2 измеряли мембранный потенциала высокоумным регистратором напряжения. ), неся туда положительный заряд, при этом происходит перезарядка мембраны внутри с «-» на «+». Na+ будет поступать до тех пор пока есть движущая сила в виде градиента концентрации ионов натрия. При достижении максимального значения мембранного потенциала (равновесного натриевого потенциала φ = +30мВ), поток натрия прекращается (натриевые каналы закрываются). Затем начинается фаза реполяризации - 2, во время которой открываются калиевые каналы, и ионы К+ большим потоком начинают выходить из клетки, унося оттуда положительный заряд (происходит снова перезарядка мембраны внутри клетки, знак «+» сменятся на «-»). Поток ионов калия на внешнюю поверхность мембраны будет происходить до тех пор пока не наступи снова потенциал покоя (равновесный калиевый потенциал).
), неся туда положительный заряд, при этом происходит перезарядка мембраны внутри с «-» на «+». Na+ будет поступать до тех пор пока есть движущая сила в виде градиента концентрации ионов натрия. При достижении максимального значения мембранного потенциала (равновесного натриевого потенциала φ = +30мВ), поток натрия прекращается (натриевые каналы закрываются). Затем начинается фаза реполяризации - 2, во время которой открываются калиевые каналы, и ионы К+ большим потоком начинают выходить из клетки, унося оттуда положительный заряд (происходит снова перезарядка мембраны внутри клетки, знак «+» сменятся на «-»). Поток ионов калия на внешнюю поверхность мембраны будет происходить до тех пор пока не наступи снова потенциал покоя (равновесный калиевый потенциал). . Т.е можно сказать, что наибольший вклад в значение мембранного потенциала φ при возбуждении мембраны вносят ионы Na+. Видно, что проницаемость для ионов Na увеличилась в 500 раз.
. Т.е можно сказать, что наибольший вклад в значение мембранного потенциала φ при возбуждении мембраны вносят ионы Na+. Видно, что проницаемость для ионов Na увеличилась в 500 раз.
 - ток через мембрану,
- ток через мембрану,  - ёмкость мембраны,
- ёмкость мембраны,  сумма ионных токов через мембрану, которая складывается из тока для ионов K+, тока Na+ и тока Cl- (ток утечки).
сумма ионных токов через мембрану, которая складывается из тока для ионов K+, тока Na+ и тока Cl- (ток утечки). ,
,  - проводимость мембраны.
- проводимость мембраны.  равновесный потенциал Нернста.
равновесный потенциал Нернста.


