e) Продукт 2, Продукт 5
f) Продукт 5, Продукт 6 g) Продукт 2, Продукт 3, Продукт 4, Продукт 5 h) Продукт 2
Задачи по теме "Метод построения дерева решений"
Задача 1. Рассматривается ситуация торгового агента, который решает, лететь ему самолетом или ехать поездом за город, где находится потребитель. Если погода будет хорошей, он может лететь и потратить на всю дорогу от ворот до ворот 2 ч, а если придется ехать поездом - 7 ч. Если он поедет поездом, то потеряет день на месте его работы, который, по его оценке, мог бы увеличить сбыт на 1500 долл. По оценке иногородний потребитель должен вручить ему заказ на 3000 долл., если он лично посетит клиента. Если он запланирует лететь к клиенту, и потом самолет вынужден будет приземлиться из-за тумана, придется заменить личное посещение телефонным звонком. Это приведет к уменьшению заказа иногороднего клиента до 500 долл., зато агент сможет обеспечить заказы на 1500 долл. дома. Предположения относительно вероятности тумана (который скажется на самолете, но не на поезде) - 10 % и ясной погоды - 90 %. Необходимо определить правильное решение: добираться к клиенту на поезде или на самолете.
Решение: Построим дерево решений для выбора оптимальной стратегии: Обозначим все возможные исходы событий: 1. Если торговый агент летит на самолете в ясную погоду: объем заказа в этом случае составит: 3000 $ (за личное посещение) + 1500 $ (за дополнительный день посещения) = 4500 $. 2. Если торговый агент поедет на поезде (и в ясную погоду, и в дождь), объем заказа составит 3000 $ (за личное посещение). 3. Если торговый агент полетит на самолете и погода будет дождливой (нелетной). Объем заказа будет равен 500 $ (уменьшенный заказ из-за непосещения клиента) + 1500 $ заказы, обеспеченные дома.
Построим дерево решений.
Наиболее вероятный объем заказа (выигрыш) при поездке на поезде: 3000*0,9 + 3000*0,1 = 3000 $. Наиболее вероятный объем заказа (выигрыш) при поездке самолетом: 4500*0,9 + 2000*0,1 = 4250 $. Вывод: более высокий вероятный выигрыш торговый агент получит при поездке на самолете. Решение принимается в сторону поездки самолетом.
Задача 2. Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов за то, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?
Решение: Построим дерево решений для всех возможных исходов событий.
Рассматриваются следующие исходы: Строить или не строить установку; монтировать или не монтировать линию; линия работает и линия не работает. Если мы строим установку, она работает и монтируем линию, то наиболее вероятный выигрыш (прибыль) составит 200*0,9-150*0,1 = 165 млн. руб. Если мы строим установку, она работает и линию мы не монтируем, то выигрыша нет (0). Если мы строим установку, она не работает и монтируем линию, то убыток составит 200*0,2-150*0,8 = -80 млн. руб. (полностью отказываемся от такого исхода). Если мы строим установку, она не работает и линию мы не монтируем, то выигрыша нет (0).
Если мы не строим установку и монтируем линию, то наиболее вероятный выигрыш составит 200*0,4-150*0,6 = -10 млн. руб. (убыток), т.о. полностью отказываемся от этого варианта. Если мы не строим установку и не монтируем линию, то выигрыша нет (0).
Останавливаемся на том варианте, когда мы строим установку, и если она работает - монтируем линию, а если не работает - не монтируем линию. В это случае наиболее вероятный выигрыш составит 165 * 0,5 + 0 * 0,5 - 10 = 72,5 млн. руб.
Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Вывод: принимаем решение: строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо.
Задача 3. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий. 1) Построить большой завод стоимостью M1 = 700 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R1 = 280 тысяч долларов в течение следующих 5 лет) с вероятностью p1 = 0,8 и низкий спрос (ежегодные убытки R2 = -80 тысяч долларов) с вероятностью р2 = 0,2. 2) Построить маленький завод стоимостью М2 = 300 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере T1= 180 тысяч долларов в течение следующих 5 лет) с вероятностью p1 = 0,8 и низкий спрос (ежегодные убытки Т2 = 55 тысяч долларов) с вероятностью р2 = 0,2. 3) Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p3 = 0,7 и p4 = 0,3 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p5 = 0,9 и р6 = 0,1 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет. Все расчеты выражены в текущих ценах и не должны дисконтироваться (приводиться к определенному моменту времени). Нарисовав дерево решений, определить наиболее эффективную последовательность действий, основываясь на ожидаемых доходах.
Решение: построим дерево решений для поставленной задачи.
Первое решение: строительство большого завода. Наиболее вероятный выигрыш 1400 * 0,8 - 400 * 0,2 - 700 = 340 тыс. $. Второе решение: строительство маленького завода. Наиболее вероятный выигрыш 900 * 0,8 - 275 * 0,2 - 300 = 365 тыс. $. Третье решение. Отложить решение на 1 год, тщательно проанализировав ситуацию на рынке. При третьем решении возможны следующие исходы: - строительство большого завода (при позитивной информации). Наиболее вероятный выигрыш будет в этом случае: 1120 * 0,9 - 320 * 0,1 - 700 = 276 тыс. $. - строительство малого завода (при позитивной информации). Наиболее вероятный выигрыш будет в этом случае: 720 * 0,9 - 220 * 0,1 - 300 = 326 тыс. $. - отказ от строительства (негативная информация о рынке). Выигрыш в этом случае будет равен 0. Рассматривая варианты строительства большого и малого завода, целесообразно выбрать второе (строительство малого завода), т.к. выигрыш в этом случае будет более высоким. В точке C наиболее вероятный выигрыш будет равен 326 * 0,7 + 0 * 0,3 = 228,2 тыс. $.
Сравнивая возможные выигрыши в точках A, B и C, выбираем вариант (т. B) строительства малого завода сразу. В этом случае наиболее вероятный ожидаемый выигрыш составит 365 тыс. $.
Задача 4. Перед встречей Нового года каждый планирует, где, как и с кем его провести. Использовав метод дерева решений, выбрать наиболее оптимальную стратегию, обеспечивающую наилучшее эмоциональное состояние от встречи Нового года при минимальных затратах на проведение праздника. Рассматриваются следующие варианты встречи Нового года: 1) Остаться дома. В этом случае можно встретить праздник, не приглашая гостей или все же пригласив друзей, знакомых и родственников. 2) Уехать встречать Новый год к родственникам или знакомым или в общедоступные места. Для количественной оценки эмоционального состояния встречи Нового года за абсолютное значение наибольшей удовлетворенности встречи праздника можно принять сумму, эквивалентную 10 тыс. рублей, которая сопоставима с получением благодарности и премии от руководства в размере 10 тыс. руб., успехах на работе, приведших к дополнительным доходам в размере 10 тыс. руб. и т.д.) Вероятность достижения абсолютного эмоционального состояния в Новый год: При встрече дома одному - 0,2; При встрече дома и приглашении гостей - 0,8; В случае поездки в общедоступные места - 0,5; В случае поездки к родственникам или знакомым - 0,8. Если Вы экстраверт (то есть в жизни настроены на проведение времени в компании, общении с другими людьми, друзьями, окружающими), то вероятность вашего желания провести новый год в кругу других людей - 0,8. По сложившейся традиции, принимая во внимание всю историю встреч Нового года на протяжении всей Вашей жизни, можно отметить, что в 6 случаев из 10 Вы встречали Новый год дома, а в 4 случаев из 10 - уезжали и встречали праздник в других местах. Ваши примерные расходы при встрече Нового года при различных вариантах: дома - 1500 руб.; дома с гостями - 7000 руб.; поездка в общедоступные места - 2500 руб. поездка в родственникам или знакомым - 5000 руб.
Если оценить количественно возможные эффекты от встречи праздника, то они будут следующими: 1. Вариант остаться дома и не звать гостей: 10000 * 0,2 - 1500 = 500 рублей (соотношение результата и затрат на праздник). 2. Вариант остаться дома и пригласить гостей: 10000 * 0,8 - 7000 = 1000 рублей. 3. Вариант уехать в общедоступные места: 10000 * 0,5 - 2500 = 2500 рублей. 4. Вариант уехать к родственниками или знакомым: 10000 * 0,8 - 5000 = 3000 рублей. Наиболее вероятный выигрыш, при встрече праздника дома: 500 * 0,2 + 1000 * 0,8 = 900. Наиболее вероятный выигрыш при встрече праздника вне дома: 2500 * 0,2 + 3000 * 0,8 = 2900. 0,8 - вероятность принятия решения о встрече праздника с другими людьми, 0,2 - вероятность встречи праздника в одиночку - 0,2. Итоговое решение - встреча праздника при поездке к родственникам, друзьям или в общедоступные места. В этом случае наиболее вероятный эффект от встречи нового году будет равен 900 * 0,6 + 2900 * 0,4 = 1700.
Задача 5. Вам рекомендуют сделать вакцинацию против гриппа. Однако вакцинация в отдельных случаях может вызвать температуру (вероятность повышения температуры 0,25). Вакцинация стоит 250 руб. При этом вероятность инфицирования гриппом составит 0,03. Если вакцинацию не проводить, то вероятность инфицирования гриппом составит 0,2. Потери от неблагоприятного самочувствия от температуры после проведения вакцинации - 2 рабочих дня (примерно 1500 руб. недополученного дохода от трудовой деятельности). Потери от заболевания гриппом 10 рабочих дней 9000 рублей недополученного дохода. Построим дерево решений, определить, стоит ли проводить вакцинацию против гриппа или нет.
Решение: По построенному дереву целей определим вероятности всех возможных исходов событий. Вероятность инфицирования без вакцинации - 0,2, вероятность сохранения здоровья без вакцинации - 0,8. Вероятность инфицирования после появления температуры в результате вакцинации - 0,03*0,25 = 0,0075. Вероятность наступления температуры после вакцинации и отсутствия заболевания гриппом - 0,75*0,25 = 0,2425. Вероятность инфицирования гриппом без предварительного повышения температуры после вакцинации - 0,03*0,75 = 0,0225. Вероятность неинфицирования гриппом без повышения температуры после вакцинации 0,97*0375 = 0,7275. Ожидаемые потери в случаем принятия решения не проводить вакцинация: -9000 * 0,2 + 0 * 0,8 = -1800. Ожидаемые потери в случае принятия решения проводить вакцинацию против гриппа: -10500 * 0,0075 - 1500 * 0,2425 - 9000*0,0225 + 0*0,7275 - 250 = 895. Таким образом, т.к. потери при непроведении вакцинации примерно в 2 раза выше, чем при проведении, то принимается решение: сделать вакцинацию против гриппа.
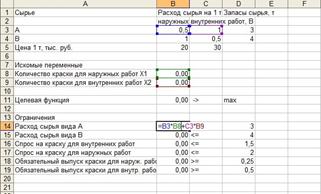
Задача 1. Коммерческому отделу поручили проанализировать совместную деятельность подразделений фабрики по изготовлению и продаже двух видов краски для внутренних (В) и наружных (Н) работ, которая поступает в продажу по цене 30 тыс. руб. и 20 тыс. руб. за 1 т. Для производства красок используют два вида сырья А и В, максимально возможные суточные запасы которых составляют 3 т и 4 т. Расходы сырья на производство 1 т красок приведены в табл. 2. Таблица 2
Изучение конъюнктуры спроса на рынке сбыта показало, что суточный спрос на краску для внутренних работ никогда не превышал спроса на краску для наружных работ более чем на 1,5 т, а спрос на краску для внутренних работ никогда не превышал 2 т в сутки. Какое количество краски каждого вида необходимо производить, чтобы доход от ее реализации был максимальным? Кроме того, известно, что план фабрики должен предусмотреть обязательный выпуск красок, производство которых не опускалось ниже 0,25 т, для красок для наружных работ и ниже 0,5 т - для красок для внутренних работ.
Решение:
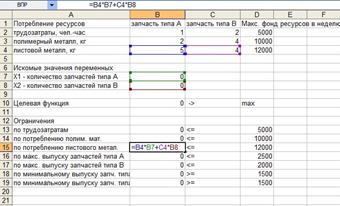
Задача 2. Фирма производит для автомобилей запасные части типа А и В. Фонд рабочего времени составляет 5000 чел.-ч в неделю. Для производства одной детали типа А требуется 1 чел.-ч, а для производства одной детали типа В - 2 чел.-ч. Производственная мощность позволяет выпускать максимум 2500 деталей типа А и 2000 деталей типа В в неделю. Для производства деталей типа А уходит 2 кг полимерного материала и 5 кг листового материала, а для производства одной детали типа В - 4 кг полимерного материала и 4 кг листового металла. Еженедельные запасы каждого материала - соответственно 10 и 12 т. Общее число производимых деталей в течение одной недели должно составлять не менее 1500 штук. Определите, сколько деталей каждого вида следует производить, чтобы обеспечить максимальный доход от продажи за неделю, если доход от продаж одной детали типа А и В составляет соответственно 110 и 150 руб.
Решение задачи в MS Excel
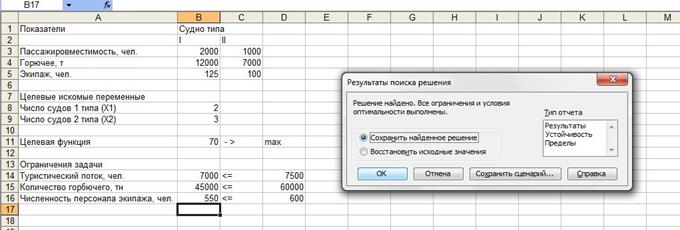
Задача 3. Туристская фирма в летний сезон обслуживает в среднем 7500 туристов в месяц и располагает флотилией из двух типов судов, характеристики которых представлены в таблице.
В месяц выделяется 60000 т горючего. Потребность в рабочей силе не превышает 600 человек. Определите количество судов I и II типа, чтобы обеспечить максимальный доход, который составляет от эксплуатации судов I типа 20 млн. руб., а II типа - 10 млн. руб. в месяц.
Решение: Решение задачи в MS Excel
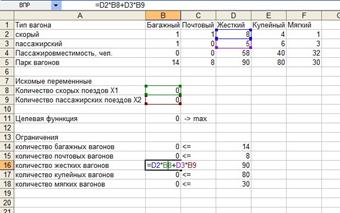
Задача 4. С Курского вокзала Москвы ежедневно отправляются скорые и пассажирские поезда. Пассажировместимость и количество вагонов железнодорожного депо станции отправления указаны в таблице.
Определите оптимальное количество пассажирских и скорых поездов, обеспечивающих максимальное количество ежедневно отправляемых пассажиров с вокзала.
Решение задачи в MS Excel
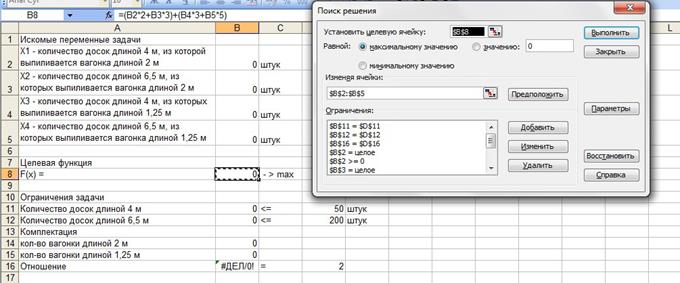
Задача 5. Предприниматель арендовал технологическую линию деревообрабатывающих станков для изготовления вагонки. Магазин «Стройматериалы» заказал комплекты из трех элементов: две вагонки длиной 2 м и одной вагонки длиной 1,25 м. Поставщик завозит на грузовом автомобиле доски толщиной 20 мм, шириной 100 мм, длиной по 6,5 м - 200 шт. и длиной по 4 м - 50 шт. Рассчитайте, как распилить доски, чтобы продать максимальное количество комплектов.
Решение задачи в MS Excel
Задача 6. Брокеру биржи клиент поручил разместить 100000 долл. США на фондовом рынке. Необходимо сформировать такой портфель с ценными бумагами, чтобы получить максимальные проценты с вложенного капитала. Выбор ограничен четырьмя возможными объектами инвестиций-акций А, В, С, Д, которые позволяют получить доход в размерах соответственно 6, 8, 10 и 9% годовых от вложенной суммы. При этом клиент поручил не менее половины инвестиций вложить в акции А и В. С целью обеспечения ликвидности не менее 25% общей суммы капитала нужно поместить в акции Д. Учитывая прогноз на изменение ситуации в будущем, в акции С можно вложить не более 20% капитала. Специфика налогообложения указывает на необходимость вложения в акции А не менее 30% капитала. Определите распределение инвестиций капитала, обеспечивающее максимальный годовой доход.
Решение задачи в MS Excel
Задача 7. Нормы затрат на производство разных видов пиццы, объемы ресурсов и стоимость приведены в таблице. Определите оптимальное количество пиццы, обеспечивающее максимальный доход от продаж.
Решение задачи в MS Excel
Задача 8. Фирма решила открыть на основе технологии производства чешского стекла, фарфора и хрусталя линию по изготовлению ваз и графинов и их декорированию. Затраты сырья на производство этой продукции представлены в таблице.
Определите оптимальный объем выпуска продукции, обеспечивающий максимальный доход от продаж, если спрос на вазы не превышает 800 шт. в неделю.
Решение задачи в MS Excel
|