МЕХАНИКА
ЛАБОРАТОРНАЯ РАБОТА № 8
определение ускорения свободного падения при помощи универсального маятника
САНКТ-ПЕТЕРБУРГ 2011 г.
Цель работы - определить ускорение свободного падения при помощи универсального маятника.
Общие сведения
Наиболее точные измерения ускорения свободного падения выполняются с помощью косвенных методов. Многие из них основаны на использовании формул для периода колебаний математического и физического маятников. Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Период колебаний математического маятника
где l - длина маятника; g - ускорение свободного падения. Ускорение g можно вычислить, измерив Т и l. Погрешность определения g в этом случае связана с тем, что реальный маятник, используемый в лабораторных условиях, может только с некоторым приближением рассматриваться как математический (чем больше l, тем точнее измерения). Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести. Период колебаний физического маятника
где J - момент инерции маятника относительно оси качаний (точки подвеса); m - его масса; l - расстояние от центра тяжести до оси качаний. Величину L = J/ (ml) называют приведенной длиной физического маятника. Она равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Зная T, m, l и J можно по формуле (2) найти ускорение свободного падения g. Массу маятника и период его колебаний можно измерить с очень высокой точностью, но точно измерить момент инерции не удается. Указанного недостатка лишен метод оборотного маятника, который позволяет исключить момент инерции из расчетной формулы для g.
Оборотный маятник (рис.1) состоит обычно из металлического стержня А, по которому могут передвигаться и закрепляться в том или ином положении грузы В 1 и В 2 и опорные призмы С 1 и С 2. Центр масс маятника - точка О. Период колебаний маятника можно менять, перемещая грузы или опорные призмы. Маятник подвешивают вначале на призме С 1 и измеряют период его колебаний Т 1. Затем маятник подвешивают на призме С 2 и измеряют период колебаний Т 2. Допустим, что нам удалось найти такое положение грузов, при котором периоды колебаний маятников Т 1 и Т 2 около призм С 1 и С 2 совпадают, т.е.
Отсюда следует, что
По теореме Штейнера
где J 0 - момент инерции маятника относительно оси, проходящей через его центр масс и параллельной оси качаний. С учетом формул (4) и (5) можно записать
или
Тогда
и
Формула (6) аналогична формуле (1) для математического маятника. Следовательно, L = l 1 + l 2 - приведенная длина физического маятника, которая, как видно из рис.1, равна расстоянию между призмами С 1 и С 2, когда Т 1 = Т 2. Это расстояние легко может быть измерено с большой точностью. Итак, измерение ускорения свободного падения g с помощью оборотного маятника сводится к измерению периодов Т 1 и Т 2 относительно призм С 1 и С 2, достижению их равенства (с помощью перемещения призм), измерению расстояния L = l 1 + l 2 между призмами и вычислению
Чтобы пояснить процедуру достижения равенства периодов Т 1 и Т 2, исследуем, как зависит период колебаний от расстояния l между центром масс и осью качаний маятника. Согласно формулам (2) и (5), имеем
Период минимален при l min = 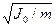 (рис.2). При Т > Т min одно и то же значение Т достигается при двух разных значениях l; одно из них больше, а другое меньше l min. Эти значения l 1 и l 2 и входят в формулу (1). (рис.2). При Т > Т min одно и то же значение Т достигается при двух разных значениях l; одно из них больше, а другое меньше l min. Эти значения l 1 и l 2 и входят в формулу (1).
Вначале измеряется период колебаний маятника Т 1 относительно призмы С 1. Затем маятник переворачивается и измеряется период колебаний Т 2 относительно призмы С 2. Если при этом получится Анализ точности измерения g методом оборотного маятника показывает, что погрешность измерения слабо зависит от точности, с которой выполняется равенство Т 1 = Т 2. Достаточно добиться того, чтобы периоды оказались равны друг другу с точностью 0,5 %. Кроме того, для получения достаточной точности измерения отношение l 1/ l 2 не должно быть ни слишком малым, ни слишком большим, желательно, чтобы 1,5 < l 1/ l 2 < 3.
Порядок выполнения работы
В основании 1 универсального маятника закреплена колонка 7, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 9 с фотоэлектрическим датчиком 10 (рис.3). Отвинчивая винт 5, верхний кронштейн можно поворачивать вокруг колонки. С одной стороны кронштейна 4 находится математический маятник 2, с другой - на вмонтированных вкладышах оборотный маятник 8. Длину математического маятника можно регулировать при помощи винта 3 и определять при помощи шкалы на колонке. Оборотный маятник выполнен в виде стального стержня, на котором крепятся две призмы (ножа) С 1 и С 2 и два диска 6. На стержень через 10 мм нанесены кольцевые нарезки, служащие для точного определения длины оборотного маятника (расстояние между призмами). Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки. Фотоэлектрический датчик соединен с привинченным к основанию универсальным электронным секундомером 11, который измеряет число колебаний n и общее время этих колебаний t. Период колебаний T = t / n. Последовательность проведения измерений с математическим маятником следующая:
2) отклонить маятник на угол примерно 5° и придерживать шарик рукой; 3) отпустив шарик, привести маятник в движение; 4) измерить время 10 колебаний (n=10); 5) повторить пп.1-4 еще пять раз; 6) по шкале на вертикальной колонке прибора определить длину маятника. При обработке результатов эксперимента определить период колебаний математического маятника T = t/n и вычислить ускорение свободного падения По результатам опыта составить таблицу:
Таблица 1
Средняя квадратичная ошибка для g
Записать окончательный результат в виде
Последовательность проведения опыта с оборотным маятником следующая: 1) поместить над датчиком оборотный маятник, повернув верхний кронштейн на 180°; 2) зафиксировать диски на стержне, чтобы один из них находился вблизи конца стержня, а другой вблизи его середины; 3) закрепить маятник на верхнем кронштейне на призме, находящейся вблизи конца стержня; 4) отклонить маятник примерно на 5° от положения равновесия и придерживать его рукой; 5) отпустив маятник, привести его в движение; 6) измерить время t 10 колебаний маятника; 7) определить период колебаний оборотного маятника T 1 = t / n; 8) снять маятник и закрепить его на второй призме; 9) измерить период Т 2, повторив пп.4-7; 10) сравнить периоды Т 2 и T 1; если Т 2 > T 1, вторую призму переместить в направлении диска, находящегося в конце стержня; если Т 2 < T 1, переместить ее в направлении середины стержня (положение дисков и первой призмы не менять); 11) снова измерить период Т 2 и сравнить его с величиной T 1; менять положение второй призмы до тех пор, пока значение периода Т 2 не станет равным значению периода T 1 с точностью до 0,5 %; 12) определить приведенную длину оборотного маятника L, измерив расстояние между призмами (по числу нарезок, которые нанесены через каждые 10 мм). При обработке результатов эксперимента вычислить ускорение свободного падения Средняя квадратичная ошибка
где Окончательный результат записать в виде
Контрольные вопросы
1. Что такое математический маятник? 2. Что такое физический маятник? 3. Почему с помощью маятников можно измерить ускорение свободного падения? 4. С чем связана погрешность определения g с помощью математического маятника? 5. С чем связана погрешность определения g с помощью физического маятника и как ее устранить? 6. В чем заключается метод оборотного маятника?
МЕХАНИКА
ЛАБОРАТОРНАЯ РАБОТА № 11
определение отношения теплоёмкости при постоянном давлении к теплоёмкости при постоянном объёме ДЛЯ воздуха методом стоячей волны
САНКТ-ПЕТЕРБУРГ 2011 г.
Цель работы - определить g = C p/ CV методом стоячей звуковой волны.
Общие сведения
Импульс силы
где S - площадь мембраны, D p – избыточное давление, обусловленное силой С другой стороны, импульс внешней силы равен приращению импульса (количества движения), которое получил газ:
где
До движения мембраны масса воздуха m в отрезке трубы длиной
или
После простых алгебраических преобразований получим
Подставив равенство (3) в формулу (4), можно записать
Если изменения плотности и давления малы (Dr << r0 и D p << p 0), то скорость распространения волны
С точки зрения термодинамики процесс распространения звуковой волны в газе можно рассматривать как адиабатический, так как изменение давления происходит так быстро, что смежные области среды не успевают обмениваться теплом. Адиабатический процесс описывается уравнением pVg = const. Так как V = M/ r (здесь М - масса газа), то p (M/r) g = const. Продифференцировав это равенство с учётом изменения давления и плотности, получим
откуда
т.е. в соответствии с формулой (6)
где r - плотность газа при данном давлении и температуре, r = p m /RT; m - молярная масса газа; R - универсальная газовая постоянная; T - абсолютная температура. Подставив r в уравнение (7), получим
откуда
Таким образом, для вычисления g необходимо определить скорость распространения звуковых колебаний. В работе эта скорость определяется методом стоячей волны. Если в трубе, один конец которой закрыт, возбудить звуковые колебания, в ней в результате наложения двух встречных волн (прямой и отражённой) с одинаковыми частотами и амплитудами будут возникать стоячие волны. В определенных точках амплитуда стоячей волны равна сумме амплитуд обоих колебаний и имеет максимальное значение; такие точки называются пучностями. В других точках результирующая амплитуда равна нулю, такие точки называются узлами. Расстояние между ближайшим узлом и пучностью равно l/4, где l - длина бегущей звуковой волны. Таким образом, измерив расстояние между узлом и пучностью или между двумя ближайшими пучностями (l/2), можно найти длину бегущей звуковой волны l. Фазовая скорость волны рассчитывается через длину волны по соотношению u = ln, (9) где n - частота колебаний.
Порядок выполнения работы
Описание экспериментальной установки.
Звуковой генератор вырабатывает синусоидальное напряжение звуковой частоты, которое подается на телефон. Переменный ток приводит в колебательное движение мембрану телефона, являющуюся излучателем звуковой волны. Отражённая от противоположной стенки трубы волна движется навстречу излучаемой и происходит их наложение. В результате в трубе возникает стоячая звуковая волна. В микрофоне происходит преобразование механической энергии волны в энергию электрического тока, величина которого измеряется микровольтметром. Частота звуковой волны устанавливается лимбом на генераторе, точное значение частоты измеряется частотомером. При перемещении телефона вдоль трубы ток в цепи микрофона будет меняться от минимального, когда микрофон попадает в узел, до максимального, когда он попадает в пучность. Таким образом, следя за показаниями микровольтметра, можно найти положения нескольких пучностей стоячей волны и вычислить ее длину. Последовательность проведения измерений: 1) включить ЗГ и частотомер в сеть, прогреть приборы в течение 3-5-ти минут; 2) после прогрева установить необходимую частоту колебаний на звуковом генераторе (указанную преподавателем), измеряя точное значение частоты частотомером; 3) перемещая телефон вдоль трубы, найти ближайшее к левому концу трубы положение телефона lk, при котором показание микровольтметра максимально, записать его в таблицу; 4) зафиксировать еще два-три положения, при которых показания микровольтметра максимальны; 5) вычислить разность между соседними отсчётами d lk = lk – lk – 1 для всех наблюдавшихся пучностей, усреднить полученные значения; 6) по среднему расстоянию между пучностями 7) повторить пп.3-6 для 4-5-ти значений частоты в интервале 1000-1800 Гц. 8) измерить температуру воздуха в помещении; 9) рассчитать g по формуле (8) при m = 2,9×10-2 кг/моль (воздух), R = 8,31 Дж/(моль×К); 10) результаты измерений и расчётов оформить в виде таблицы:
Таблица 1.
11) найти среднее значение 12) рассчитать погрешность косвенных измерения g.
Контрольные вопросы
1. Что такое теплоемкость, молярная теплоемкость, удельная теплоемкость? Как они связаны? Какова размерность теплоемкости? От чего зависит молярная теплоемкость? 2. Почему Cp > CV с точки зрения первого начала термодинамики? 3. Что такое бегущая и стоячая звуковая волна? Каковы ее основные характеристики? 4. Каков механизм распространения звуковой волны? 5. Что представляет собой звуковая волна с точки зрения термодинамики? Каким уравнением и графиками описывается рассматриваемый процесс? 6. От чего зависит скорость распространения звуковой волны?
|

 , (1)
, (1)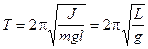 , (2)
, (2)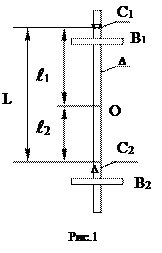 Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же. Расстояние между этими точками представляет собой приведенную длину данного маятника.
Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же. Расстояние между этими точками представляет собой приведенную длину данного маятника.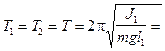
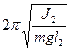 .
.  (3)
(3)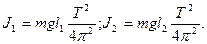 (4)
(4)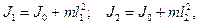 (5)
(5)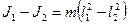
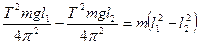 .
.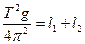
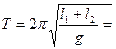
 . (6)
. (6)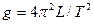 (7)
(7)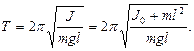
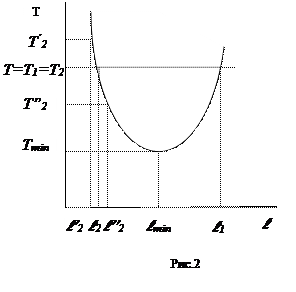
 , то этому будет соответствовать
, то этому будет соответствовать 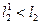 . И для того, чтобы приблизить
. И для того, чтобы приблизить 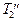 и Т 1, надо увеличить
и Т 1, надо увеличить 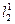 . Для этого надо призму С 2 передвинуть от середины стержня к краю. Если получится
. Для этого надо призму С 2 передвинуть от середины стержня к краю. Если получится 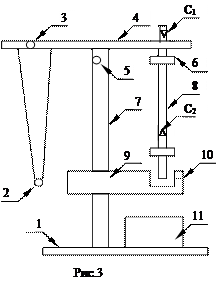 1) поместить над датчиком математический маятник, повернув соответствующим образом верхний кронштейн;
1) поместить над датчиком математический маятник, повернув соответствующим образом верхний кронштейн; для каждого измерения и среднее
для каждого измерения и среднее 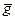 .
.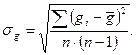
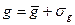 .
.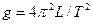 при Т = Т 1 = Т 2 и среднюю квадратичную ошибку
при Т = Т 1 = Т 2 и среднюю квадратичную ошибку 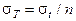 , где
, где 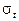 - погрешность измерения времени, оцениваемая исходя из точности прибора.
- погрешность измерения времени, оцениваемая исходя из точности прибора.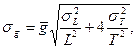
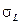 - погрешность измерения длины, оцениваемая по цене деления измерительной линейки.
- погрешность измерения длины, оцениваемая по цене деления измерительной линейки. .
.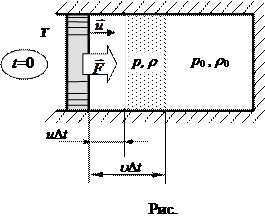 Рассмотрим, как распространяется звуковая волна в закрытой цилиндрической трубе, заполненной воздухом. В момент времени t = 0 мембрана телефона T (рис.1) начинает двигаться вправо с постоянной скоростью
Рассмотрим, как распространяется звуковая волна в закрытой цилиндрической трубе, заполненной воздухом. В момент времени t = 0 мембрана телефона T (рис.1) начинает двигаться вправо с постоянной скоростью 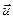 . Молекулы воздуха вблизи мембраны придут в движение и тоже будут перемещаться вправо со скоростью
. Молекулы воздуха вблизи мембраны придут в движение и тоже будут перемещаться вправо со скоростью  - скорости распространения в пространстве поверхностей, образованных частицами, совершающими колебания в одинаковой фазе.
- скорости распространения в пространстве поверхностей, образованных частицами, совершающими колебания в одинаковой фазе.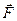 , с которой мембрана в течение времени D t давит на газ
, с которой мембрана в течение времени D t давит на газ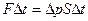 , (1)
, (1) , (2)
, (2) - плотность сжатого воздуха;
- плотность сжатого воздуха; 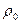 - плотность воздуха в начальный момент времени;
- плотность воздуха в начальный момент времени; 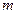 - масса сжатого воздуха;
- масса сжатого воздуха;  - длина столба воздуха (путь, который прошла волна за время
- длина столба воздуха (путь, который прошла волна за время 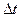 ). Объединяя равенства (1) и (2), получим
). Объединяя равенства (1) и (2), получим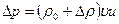 . (3)
. (3)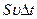 . При смещении мембраны на u D t плотность воздуха меняется, и в этом случае его массу можно представить (рис. 1)
. При смещении мембраны на u D t плотность воздуха меняется, и в этом случае его массу можно представить (рис. 1)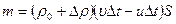 ,
,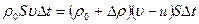 ,
,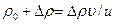 . (4)
. (4) . (5)
. (5)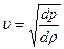 . (6)
. (6)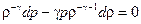 ,
,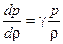 ,
,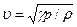 , (7)
, (7)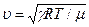 ,
,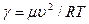 . (8)
. (8) В экспериментальную установку (рис.2) входят: стеклянная труба, в которой создаётся стоячая волна, звуковой генератор (ЗГ), микровольтметр, частотомер (Ч). В стеклянную трубу вмонтированы неподвижный микрофон (М) и телефон (Т), который может свободно перемещаться вдоль оси трубы.
В экспериментальную установку (рис.2) входят: стеклянная труба, в которой создаётся стоячая волна, звуковой генератор (ЗГ), микровольтметр, частотомер (Ч). В стеклянную трубу вмонтированы неподвижный микрофон (М) и телефон (Т), который может свободно перемещаться вдоль оси трубы. рассчитать длину бегущей волны l= 2×
рассчитать длину бегущей волны l= 2× 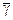 ;
;


