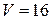Задача о ранце. Имеется ранец объем которого .
Имеется ранец объем которого Пусть имеется список товаров, которые мы хотим положить в ранец
Проблема возникает только тогда, когда общий объем товаров превышает объем ранца. Эта задача о выборе наилучшего варианта загрузки ранца. Пусть Чем мы управляем в этой модели? Вектором Как мы управляем? При заполнении ранца, мы ограничены его объемом, т.е.:
Зачем решается задача? Чтобы общая полезность товаров, наполняющих ранец, была максимальной, т.е.
Эту задачу можно формулировать как задачу выбора портфеля инвестиции. В этом случае
Тогда задача, которая имеет ту же самую математическую постановку, может быть сформулирована следующим образом: Вставить инвестиционный проект таким образом, чтобы суммарная прибыль от вложений была бы максимальной. Различных вариантов в этой задаче 2N, часть вариантов недопустима, т. к. они могут нарушать ограничение по объему наполнения, это так же позволит отсекать некоторые ветви. Ветвление в этой задаче организуется следующим способом: Сначала все множество вариантов разбивается на 2 подмножества: – Берем товар в ранец, – Не берем второй товар, последующее ветвление ведется аналогично. Для каждого товара первоначально рассчитывается удельная полезность товара:
Т.е. полезность единицы объема товара, и список товаров ранжируется по убыванию этой величине, т.к. товар с большей удельной полезностью для нашей цели предпочтительней. После этого применяется метод ветвей и границ. Пример решения задачи о ранце. Объем ранца
Упорядочим таблицу, в результате получим:
|

 .
. ,
, — объем i -го товара,
— объем i -го товара,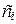 — полезность конечного товара.
— полезность конечного товара. , если товар не берется в ранец, и
, если товар не берется в ранец, и  , если товар принимается.
, если товар принимается. .
.

 — объем средств для вложения в i -й проект,
— объем средств для вложения в i -й проект, — прибыль i -го инвестиционного проекта.
— прибыль i -го инвестиционного проекта.