Примечания автора. 1 Это утверждение является некоторым упрощением, так как эйнштейновский эффект (правда, в два раза слабее) можно вывести из классической теории
1 Это утверждение является некоторым упрощением, так как эйнштейновский эффект (правда, в два раза слабее) можно вывести из классической теории, если принять корпускулярную теорию света. 2 См., например, мою работу: Popper K. R. The Open Society and Its Enemies, vols. I-II. London, 1945 (русский перевод: Поппер Карл Р. Открытое общество и его враги, т. 1-2. М., 1992, гл. 15, разд. III и прим. 13-14). 3 «Клинические наблюдения», подобно всем другим наблюдениям, являются интерпретациями в свете теорий (см. далее разд. IV) и только по этой причине их склонны рассматривать как подтверждения тех теорий, в рамках которых они интерпретируются. Однако действительное подтверждение можно получить только из тех наблюдений, которые были специально предприняты для проверки (с целью «опровержения» теории). 4 Иллюстрацией этого утверждения может служить астрология — типичная псевдонаука в наши дни. Со стороны аристотелианцев и (113:) других рационалистов вплоть до Ньютона она подвергалась нападкам по ошибочным основаниям — за ее ныне признанное утверждение о том, что планеты оказывают «влияние» на земные («подлунные») события. Фактически ньютоновская теория гравитации и, в частности, лунная теория приливов исторически были детищем астрологических идей. По-видимому, Ньютон очень не хотел принимать теорию, восходящую к тому же источнику, что и теории, объясняющие, например, возникновение эпидемий гриппа «влиянием» звезд. И Галилей, несомненно, по тем же основаниям отвергал лунную теорию приливов, и его опасения по поводу результатов Кеплера легко объясняются его опасениями в отношении астрологии. 5 Logic of Scientific Discovery (1959, 1960, 1961) представляет собой английский перевод моей книги Logik der Forschung (1934) с некоторыми новыми примечаниями и добавлениями, включая упомянутое письмо к издателю Erkenntnis, которое впервые было опубликовано в Erkenntnis, 3, 1933, pp. 426. Относительно упомянутой неопубликованной моей книги см. статью Карнапа «О протокольных предложениях», Erkenntnis, 3, 1932, pp. 215-28, в которой он дает описание предложенной мною теории и соглашается с ней. Он называет мою теорию «процедурой В» и, в частности, говорит: «Исходя из концепции, отличной от концепции Нейрата (который разработал «процедуру А», по выражению Карнапа), Поппер развил процедуру В как часть своей системы» (р. 224). И после подробного описания моей теории проверок Карнап следующим образом подводит итог своим рассуждениям: «Рассмотрев представленные здесь различные аргументы, я прихожу к выводу о том, что вторая форма языка с процедурой В, описанная здесь, представляется наиболее адекватной среди всех форм научного языка, выдвинутых к настоящему времени... в теории познания» (р. 228). Эта статья Карнапа содержит первое печатное изложение моей теории критических проверок (см. также мои критические замечания в «Логике научного открытия», прим. 1 в разделе 29, где дату «1933» следует читать как «1932», и главу 11 ниже, текст к прим. 39). 6 Витгенштейн приводит следующий пример бессмысленного псевдопредложения: «Сократ тождествен». Предложение «Сократ нетождествен», очевидно, также должно быть бессмысленным. Таким образом, отрицание бессмысленного предложения дает бессмысленное, а отрицание осмысленного предложения также будет осмысленным. Однако, как впервые было указано в моей «Логике научного открытия», а затем и моими критиками, отрицание проверяемого (или фальсифицируемого) высказывания не обязательно должно быть проверяемым. Легко представить, какая путаница возникает в том случае, если проверяемость считают критерием значения, а не демаркации. 7 Самый свежий пример неправильного понимания истории этой проблемы дает статья: A.R. White. Note on Meaning and Verification. — (114:) Mind, 63, 1954, pp. 66 ff. Статья Дж.Л. Эванса в Mind, 62, 1953, pp. 1 ff., которую критикует Уайт, на мой взгляд, превосходна и весьма глубока. Понятно, конечно, что ни один из авторов не может вполне воссоздать историю (некоторые указания по этому поводу можно найти в моей работе «Открытое общество и его враги», прим. 46, 51 и 52 гл. 11; более полный анализ см. в гл. 11 настоящей книги). 8 В работе «Логика научного открытия» я проанализировал некоторые возможные возражения против моей концепции и ответил на них. Впоследствии эти возражения действительно были выдвинуты, однако без ссылки на мои ответы. Одно из них заключается в утверждении, что фальсификация закона природы столь же невозможна, как и его верификация. Ответ на это возражение состоит в указании на то, что в нем смешиваются два совершенно разных уровня анализа (подобно тому, как это происходит с утверждением, что математические доказательства невозможны, ибо, сколько бы их ни проверяли, у нас никогда не будет полной уверенности в том, что мы не пропустили ошибки). На первом уровне имеет место логическая асимметрия: одно сингулярное высказывание, скажем, о перигелии Меркурия, может формально фальсифицировать законы Кеплера, однако их нельзя формально верифицировать никаким числом сингулярных высказываний. Попытка уменьшить эту асимметрию может привести лишь к путанице. На втором уровне мы можем испытывать колебания по поводу любого высказывания, включая даже самые простейшие высказывания наблюдения; в этом случае мы осознаем, что каждое высказывание включает интерпретацию в свете теорий и потому проблематично. Это обстоятельство не влияет на указанную фундаментальную асимметрию, но оно имеет важное значение: большая часть анатомов, исследовавших сердце до Гарвея, видела ошибочные вещи, а именно те, которые они ожидали увидеть. Не может существовать вполне надежного наблюдения, не подверженного опасности ошибочных интерпретаций. (В этом состоит одна из причин, объясняющих бесплодность теории индукции.) «Эмпирический базис» в значительной мере состоит из смеси теорий низкой степени универсальности (описывающих «воспроизводимые эффекты»). Однако независимо от этого, фактом является то, что какой бы базис ни принял на свой риск исследователь, он может проверить свою теорию, только пытаясь опровергнуть ее. 9 Юм говорил не о «логических», а о «демонстративных» аргументах, употребляя терминологию, которая, как мне кажется, не вполне верна. Следующие две цитаты взяты из «Трактата о человеческой природе», кн. 1, часть 3, разделы 6 и 12 (Юм Д. Соч. в 2-х томах, т. 1. М., Мысль, 1965). (Курсив Юма.) 10 Эта и следующие цитаты взяты из указ. Соч., разд. 6. См. также «Исследование человеческого понимания», разд. 4, часть 2. (115:) 11 «Трактат о человеческой природе» — там же, гл. 13, правило 4, с. 282. 12 F. Bage, Zur Entwicklung, etc., Zeitschrift f. Hundeforschung, 1933; см. также: D. Katz, Animals and Men, ch. vi, footnote. 13 См. раздел 30 «Логики научного открытия». 14 Katz, loc. cit. 15 Кант был убежден в том, что динамика Ньютона априорно верна (см. его работу «Метафизические начала естествознания», опубликованную в период между первым и вторым изданиями «Критики чистого разума»). Однако если справедливость теории Ньютона можно объяснить, как он считал, тем, что наш разум налагает свои законы на природу, то отсюда, как мне представляется, следует, что наш разум должен достигать в этом успеха. Но в таком случае трудно понять, почему априорное знание — такое, как теория Ньютона, — добывается с таким трудом (несколько более развернутое изложение этого вопроса можно найти в гл. 2, раздел X и гл. 7 и 8 настоящей книги). 16 Диссертация, представленная под названием Gewohnheit und Gesetzerlebnis в Венский педагогический институт (неопубликована). 17 Дальнейшие комментарии по этому поводу можно найти в гл. 4 и 5 ниже. 18 Мах Born. Natural Philosophy of Cause and Chance, Oxford, 1949, p. 7. 19 Natural Philosophy of Cause and Chance, p. 6. 20 Я не сомневаюсь в том, что Борн и многие другие ученые согласятся с тем, что теории принимаются лишь временно. Однако широко распространенная вера в индукцию показывает, что мало кто замечает, к каким важным следствиям приводит эта точка зрения. 21 Витгенштейн придерживался этого взгляда еще в 1946 году; см. примечание 8 к гл. 2 ниже. 22 См. примечание 5 выше. 23 «Логика научного открытия» (см. примечание 5 выше), гл. X, в частности, разделы 80—83, а также раздел 34. См. также мою заметку A Set of Independent Axioms for Probability, Mind, N.S. 47, 1938, p. 275. С некоторыми изменениями эта заметка была перепечатана в новом приложении *ii к «Логике». См. также следующие примечания к настоящей главе. 24 Определение в терминах теории вероятностей (см. следующее примечание) величины C(t, e), то есть степени подкрепления теории относительно свидетельства е, удовлетворяющее требованиям, перечисленным в моей «Логике научного открытия», разд. 82-83, выглядит следующим образом: C(t, е) = E(t, е) ( 1+ P(t)P(t, e)), где E(t, е) = (Р(е, t) — Р(е))/(Р(е, t) + Р(е)) является (неаддитивной) мерой объяснительной силы t относительно е. Следует заметить, что (116:) величина C(t, e) не является некоторой вероятностью, так как может принимать значения от –1 (опровержение t посредством е) до C(t, t) < +1. Высказывания t, имеющие форму законов и поэтому неверифицируемые, не могут получить даже значения C(t, е) = C(t, t) при любом эмпирическом свидетельстве е. C(t, t) представляет собой степень подкрепляемости теории t, и она равна степени проверяемости t или содержанию t. Мне представляется, однако, что требования, включенные в пункт (6), сформулированный выше в конце разд. I, делают невозможной полную формализацию идеи подкрепления (или, как я раньше предпочитал говорить, идеи подтверждения). (Добавлено в 1955 году к первой корректуре данной статьи.) См. также мою заметку Degree of Confirmation, British Journal for the Philosophy of Science, 5, 1954, pp. 143 ff (См. также 5, pp. 334). После этого я упростил данное определение следующим образом (B.J.P.S., 1955, 5, р. 359):
Относительно последующих улучшений см. B.J.P.S., 6, 1955, р. 56. 25 См. мою статью в Mind, loc. cit. Систему аксиом, сформулированную в этой работе для элементарных (то есть дискретных) вероятностей, можно упростить следующим образом ( (А1) (А2) (A3) (В1) (В2) (В3) (C1) Если (С2) Если Аксиома (С2) в этой форме справедлива только для финитной теории, ее можно опустить, если мы готовы довольствоваться условием
ни его ослабленного следствия:
из которого (В3) вытекает непосредственно (путем подстановки вместо (Добавлено в 1955 году; см. также примечание 31 ниже). Позднее я построил систему аксиом для относительной вероятности, которая справедлива для конечной и бесконечной систем (и в которой абсолютную вероятность можно определить так, как это сделано в предпоследней формуле выше). Аксиомы этой системы таковы: (В1) (В2) Если (В3) (C1) (D1) Если (E1) Это небольшое улучшение системы, опубликованной в B.J.P.S., 6, 1955, pp. 56 f.; «Постулат 3» здесь назван «D1». 26 См.: «Логика научного открытия», раздел 53; см. новое приложение xvi. 27 См.: «Логика научного открытия», разделы 41-46; см. также гл. 10, раздел xviii ниже. 28 Для случая задачи многих тел упомянутые противоречия были указаны Дюгемом в работе «Цель и строение физической теории». Для задачи двух тел противоречие возникает в связи с третьим законом Кеплера, который для задачи двух тел можно переформулировать следующим образом: «Пусть S — любое множество пар тел таких, что одно из тел каждой пары имеет массу нашего Солнца; тогда для любого множества S, а3/Т2 — константа». Ясно, что это противоречит ньютоновской теории, которая для соответствующих единиц дает равенство а3/Т2 = т0 + m1 (где т0 — масса Солнца, являющаяся константой, а т1 — масса второго тела, которая изменяется в зависимости от выбранного тела). Однако равенство «а3/Т2 = константа» будет, конечно, прекрасным приближением при условии, что изменяющаяся масса второго тела пренебрежимо мала по сравнению с массой Солнца (см. также мою статью The Aim of Science, Ratio, 1, 1957, pp. 24 к раздел 15 «Postscript» моей «Логики научного открытия»). 29 См. мою работу «Нищета историцизма», 1957, раздел 28 и примечания 30-32, а также «Приложение» к т. 2 моего «Открытого общества» (добавлено к 4-му изданию 1962 г.). 30 См. «Нищета историцизма», раздел 32; «Логика научного открытия», раздел 8; «Открытое общество», гл. 23 и «Приложение» к т. 2 (четвертое издание). (118:) 31 Проблема (13) была добавлена в 1961 году. С 1953 года, в котором была прочитана эта лекция, и с 1955 года, когда я читал корректуру, список приведенных в этом приложении проблем значительно возрос, и некоторые более поздние идеи, касающиеся не указанных здесь проблем, можно найти в данной книге (см. особенно гл. 10 ниже) и других моих книгах (см., в частности, новые приложения к «Логике научного открытия» и новое «Приложение» к т. 2 «Открытого общества»). См. также мою статью Probability Magic, or Knowledge out of Ignorance, Dialectica, 11, 1957, pp. 354-374. (119:)
|


 обозначает дополнение х; ху — пересечение или конъюнкцию х и у):
обозначает дополнение х; ху — пересечение или конъюнкцию х и у): (коммутативность)
(коммутативность) (ассоциативность)
(ассоциативность) (тавтология)
(тавтология) (монотонность)
(монотонность) (сложение)
(сложение) и
и  (умножение)
(умножение) , то
, то 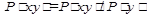 (определение относительной вероятности)
(определение относительной вероятности) , то
, то 
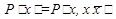 ,
, ,
, его определения). Таким образом, подобно всем другим (117:) аксиомам, за исключением, может быть (С2), аксиома (В3) выражает часть подразумеваемого значения понятия вероятности, и мы не должны считать
его определения). Таким образом, подобно всем другим (117:) аксиомам, за исключением, может быть (С2), аксиома (В3) выражает часть подразумеваемого значения понятия вероятности, и мы не должны считать  или
или  , которые выводимы из (В1) с (В3) или с (Cl) и (С2), «несущественными соглашениями» (как считают Карнап и другие).
, которые выводимы из (В1) с (В3) или с (Cl) и (С2), «несущественными соглашениями» (как считают Карнап и другие).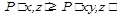
 , то
, то 


 , то
, то 
 .
.


