РАСЧЕТ ОСВЕЩЕННОСТИ ОТ СВЕТЯЩИХ ПОВЕРХНОСТЕЙ РАВНОМЕРНОЙ ЯРКОСТИ

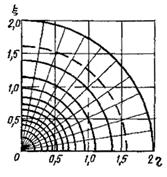
7.11. Освещенность Е в точке А расчетной плоскости, создаваемая светящей поверхностью размером а х b (рис. 89) определяется из уравнения

Е = l _о f (a / h _р, b / h _р), (83)

где L _o - яркость по нормали к светящей поверхности.

При равномерной и одинаковой во всех направлениях L _o и телесном угле в стерадианах значение светимости М определяется по формуле

М =p L _o; L _o= M /p.

Следовательно, если f (a / h _р, и b / h _р) обозначить через q, то уравнение (83) примет вид

E=Mq. (84)

На основании уравнения (84) построены номограммы для определения освещенности на плоскости, параллельной и перпендикулярной светящей поверхности. По осям абсцисс и ординат номограммы отложены относительные размеры светящего прямоугольника (а' = a / h _р и b '= b / h _p) и построены кривые равных значений q.

Номограмма рис. 89 позволяет определить коэффициент освещенности от светящего прямоугольника, параллельного расчетной плоскости. Номограмма рис. 90 предназначена для определения коэффициента освещенности от светящих прямоугольников, перпендикулярных расчетной плоскости.

Расчет освещенности с помощью приведенных номограмм допустим лишь в частном случае, когда проекция вершины светящего прямоугольника совпадает с расчетной точкой. Однако к этому частному случаю можно свести любой случай, встречающийся на практике. Светящий прямоугольник может быть разбит на отдельные прямоугольники, вершина которых совпадает с точкой расчета А (рис. 91). В этом случае q при светящем прямоугольнике, расположенном, как показано на рис. 91,а, будет иметь значение

q ₁₂₃₄= q ₂₅₇₉- q ₁₅₇₈- q ₄₆₇₉+ q ₃₆₇₈;

для ситуации, показанной на рис. 91,б,

q ₁₂₃₄= q ₁₅₇₉+ q ₅₂₉₈+ q ₇₉₃₆+ q ₉₈₆₄.

Рис. 90. Номограмма для расчета освещенности от равнояркого светящего прямоугольника, перпендикулярного расчетной плоскости

Рис. 91. Варианты размещения светящих прямоугольников

Рис. 92. Измерительная номограмма для расчета освещенности от светящих поверхностей при светораспределении светящего элемента I = I _ocos³a

Для определения q могут применяться также измерительные номограммы. На рис. 92 приводится одна из таких номограмм, рассчитанная для светораспределения I a= I _oсos³a, которая предназначена для определения q при расчете освещенности от потолков и панелей, перекрытых экранирующими решетками с защитным углом около 45°. Рис. 92 представляет собой один из четырех квадрантов номограммы, которая в полном объеме содержит 500 элементов (четырехугольных, у вершины - треугольных). Элементы, ограниченные с одной стороны штриховой дугой, считаются за 0,5. На горизонтальной освещаемой плоскости произвольно выбирается направление осей координат х, у с началом в расчетной точке. Контуры излучателя наносятся на сетке номограммы по координатам их вершин

x= х / h _p; h= y / h _p.

Если в пределах этих контуров вмещается z элементов графика, то q = z /500. Измерительная номограмма пригодна для определения освещенности от поверхностей любой формы.

Пример 7. Прямоугольное помещение площадью 20´40 м² и высотой 4 м освещается светящей панелью, расположенной в плоскости потолка помещения (рис. 93). Размеры панели 8´16 м². Светимость панели 200 лм/м². Определить освещенность в центре помещения на уровне пола, принимая коэффициент запаса К _з=1,5.

Разбиваем светящий прямоугольник на четыре части так, чтобы проекция одной из вершин каждой из них совпала с расчетной точкой. Стороны полученных прямоугольников находим на рис. 93: а =4 м, b =8 м.

Соответственно относительные размеры сторон

а '= а / h _р=4/4=1,0; b' = b / h _p=8/4=2,0.

По номограмме рис. 89 находим значение q для одного такого прямоугольника: q= 16,5%.

Так как размеры всех четырех прямоугольников одинаковы, то освещенность в расчетной точке А равна:

Е =4 qM / К _з=4·0,165·200/1,5»88 лк.