Алгоритм Крускала

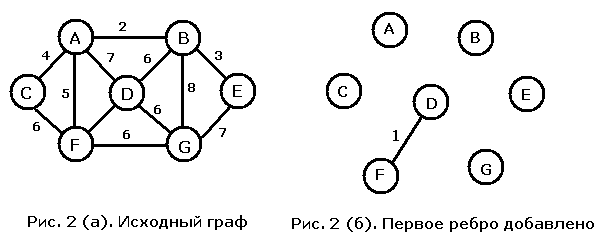
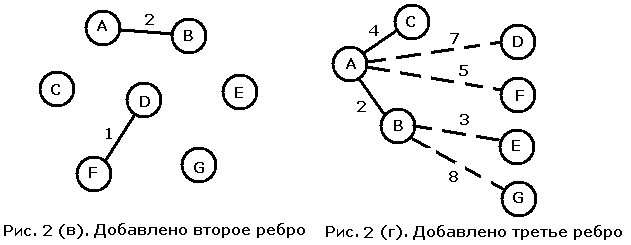
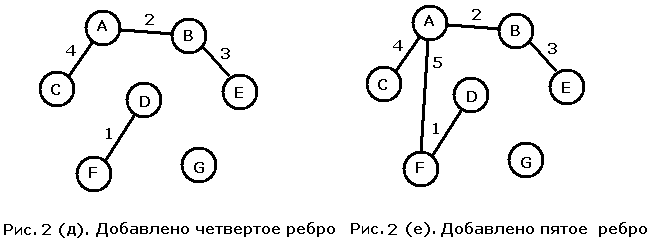
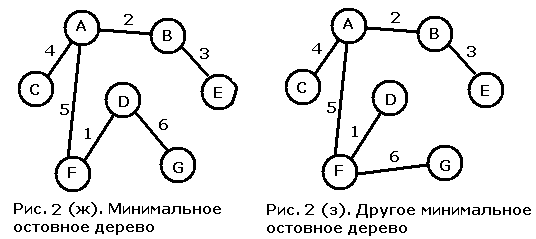
Алгоритм Дейкстры-Прима начинает построение МОД с конкретной вершины графа и постепенно расширяет построенную часть дерева; в отличие от него алгоритм Крускала делает упор на ребрах графа.

В этом алгоритме мы начинаем с пустого дерева и добавляем к нему ребра в порядке возрастания их весов пока не получим набор ребер, объединяющий все вершины графа. Если ребра закончатся до того, как все вершины будут соединены между собой, то это означает, что исходный граф был несвязным, и полученный нами результат представляет собой объединение МОД всех его компонент связности.

Мы работаем с тем же графом (см. рис. 2 (а)), что и при описании алгоритма Дейкстры -Прима. Начнем с ребра наименьшего веса, то есть с ребра DF. Начальная ситуация изображена на рис. 2 (б).

Следующим добавляется ребро веса 2, соединяющее вершины A и B (рис. 2 (в)), а затем - ребро веса три, и мы получаем ситуацию с рис. 2 (г).

К результирующему графу последовательно добавляются ребра весов 4 и 5 (рисунки 2 (д) и (е)). Несоединенной осталась лишь вершина G. Следующими мы должны рассмотреть ребра веса 6.

Два из четырех ребер веса 6 следует отбросить, поскольку их добавление приведет к появлению цикла в уже построенной части МОД. Присоединение ребра CF создало бы цикл, содержащий вершину A, а присоединение ребра BD - цикл, содержащий вершины A и F. Обе оставшиеся возможности подходят в равной степени, и, выбирая одну из них, мы получаем либо МОД с рис. 2 (ж), либо МОД с рис. 2 (з).

Задания для самостоятельного выполнения

Задание 1. Телевизионная компания планирует подключение к кабельной сети пяти новых районов. Структура планируемой сети и расстояния между пунктами заданы рисунком.

 

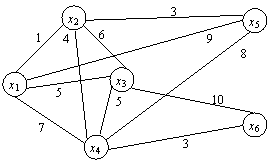
Требуется спланировать наиболее экономичную кабельную сеть.

Задание 2. Имеется 6 городов, которые нужно объединить в единую телефонную сеть. Структура планируемой сети и расстояния между городами заданы рисунком.

 

Как соединить города так, чтобы суммарная стоимость соединений (телефонного кабеля) была минимальна?

Задание 3. Построить минимальное остовное дерево для следующего графа и найти его вес.

а) б)