Вывод рабочей формулы
Рассмотрим метод построения изображения в линзе. Ход лучей 1–1′, 2–2′, 3–3′ показан на Рис. 3.
Все эти лучи пересекаются в точке S′, которая является изображением источника света S. Расстояния от предмета до линзы и от линзы до изображения (Рис. 3) связаны с фокусным расстоянием формулой линзы:
Выразим из этого уравнения F, получим:
Уравнение (4) позволяет определить фокусное расстояние линзы, измерив значения d и f. Если расстояние между предметом и изображением больше учетверенного расстояния от линзы до изображения, то, перемещая линзу вдоль ее главной оптической оси, на экране можно получить увеличенное или уменьшенное изображение предмета. При этом источник света и экран остаются неподвижными. Рис. 4 показывает ход лучей от источника до экрана при получении увеличенного и уменьшенного изображения предмета. Обозначим d 1 — расстояние от предмета и f 1 — расстояние от экрана до линзы в первом положении; d 2 — расстояние от предмета и f 2 — расстояние от экрана до линзы во втором положении. Запишем формулы тонкой линзы для обоих положений:
Здесь: f 1 = L – d 1, d 2 = d 1 + l и f 2 = L – d 2. Выразим из (5) и (6) равенств F:
— для первого положения и
— для второго положения. Т. к. левые части равны, то равны и правые. Приравняем их и подставим вместо d 2, f 2 и f 1 их выражения через d 1, получим:
Сократим на L, раскроем скобки и приведём подобные: 2 d 1 l = Ll – l 2. Выразим d 1:
Преобразуя это равенство и выражая F, получим:
Таким образом, можно определить фокусное расстояние линзы, измерив перемещение линзы l и расстояние между предметом и экраном L.
|

 Рис. 3
Рис. 3


 Рис. 4
Рис. 4
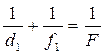 ,
,
 ,
,


 .
. , и подставим в (5):
, и подставим в (5):
 .
.



