Гомель, 2011
Если задача статически определима, т.е. функция Q(r) известна, то из (7) с учетом (8а), (9а) получаем уравнение типа Ламе
интегрируя которое имеем
Такой же результат получаем, естественно, дифференцируя (2*) с учетом (3*) и (8а). В качестве примера рассмотрим задачу расчета плоского днища цилиндрической оболочки (схема в первом примере граничных условий). Здесь: Подставляя в (8а), (9а) находим
Подставляем в (4а), (5а)
В месте сопряжения с оболочкой
Сравнивая с напряжениями в оболочке, получаем, что напряжения в свободном днище в В заключении определим перемещения. Подставляя полученное выражение для θ в (1*), интегрируя, с учетом граничного условия
Напомним, что расчет проведен в предположении свободного закрепления пластины в направлении радиуса.
Министерство образования Республики Беларусь Учреждение образования «Гомельский государственный университет имени Франциска Скорины» В. Ф. БАГИНСКИЙ ТАКСАЦИЯ ЛЕСА Учебное пособие для студентов высших учебных заведений по специальностям «Лесное хозяйство», «Лесоинженерное дело» Гомель, 2011
УДК 630*52(075.) ББК 43я73 А 92 Рецензенты: профессор кафедры лесоустройства и лесной таксации учреждения образования «Белорусский государственный технологический университет», доктор сельскохозяйственных наук, профессор, Заслуженный лесовод Республики Беларусь О.А. Атрощенко; главный научный сотрудник ГНУ Института леса НАН Беларуси, доктор биологических наук В.Б. Гедых.
|

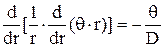 ,
,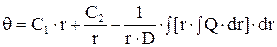 . (5*)
. (5*)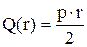 ,
, 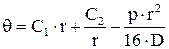 ,
, 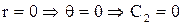 ,
,  ,
,  .
. .
.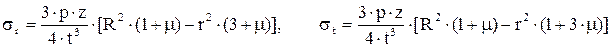 .
.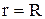 при
при 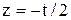 получаем
получаем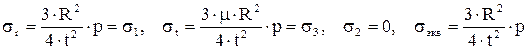 .
. больше. Именно по этому в сосудах используют сферические или полусферические днища.
больше. Именно по этому в сосудах используют сферические или полусферические днища. получаем
получаем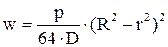 .
.


