Ошибки измерений
Любые наблюдения и измерения могут иметь определенную точность и содержать ошибку, т.к. истинного значения измеряемой величины мы не можем точно знать – процесс познания бесконечен. К.Е. Никитин, А.З. Швиденко выделяют следующие ошибки лесоводственной информации. · Ошибки наблюдений и измерений. · Погрешности инструментов и приборов. · Ошибки моделирования. · Ошибки вычислительных операций. Диаметр дерева изменяется в разных направлениях. К тому же величина измерений зависит от времени суток. Определенную погрешность измерений имеют инструменты, На ошибку измерений влияет схема выборки и т.д. В геодезии понятие «ошибка» означает отклонение от «истинного» значения. Это понятие не ассоциируется с идеей «неправильное, ошибочное» измерение, а связано с его «неточностью». Причины такой неточности измерений могут быть следующие. · Особенности объекта измерения. Некоторые физические объекты могут быть измерены более точно, т.к. они имеют более правильную геометрическую форму и постоянные границы объекта. Объем дерева или его части оценить труднее. Обычно объемы стволов приближают к формулам правильных тел вращения: параболоид, цилиндр, нейлоид. В то же время образующая древесного ствола, особенно растущего дерева, варьирует значительно. Страта леса выполняется следующим образом: делают оценку типов леса, а затем организуют страты, объединяя однородные типы леса, возраста насаждений в одну страту. Площадь поперечного сечения ствола принимают за круг, хотя форма ствола может значительно отличаться от круга> · Неточность измерительных инструментов и приборов. Обычная мерная вилка дает систематическую ошибку в +3 %, точность высотомеров – 0,5 – 1 м. · Влияние физических и топографических условий на измерения. Температура, влажность воздуха, погодные условия (солнце, дождь и т.д.) влияют на точность измерений и деформацию инструмента, · Неопределенность в процессе измерений. Она заключается в том, что измерения диаметров деревьев делают в разных направлениях (север, юг, запад, восток) и группируют в ступени толщины. Проводят округления в показаниях высотомеров и т.д. · Точность человеческого восприятия – это особенно относится к оптическим приборам: реласкоп, призмы и т.д. Многие из перечисленных источников ошибок измерений оценить весьма трудно, а иногда практически невозможно. Но наша задача выявить различные виды ошибок измерений и их влияние на конечный результат. Ошибки измерений и наблюдений можно подразделить на следующие виды. · Грубые ошибки – обычно неверная запись результатов. Методом контроля здесь явится повторная проверка записи другими исполнителями. · Односторонние ошибки постоянной величины определенного знака (положительные или отрицательные). Это – систематические ошибки, вызванные неисправностью прибора, недостатком метода, несоответствием математической модели т.д. Так, если мерная вилка имеет большой люфт, то диаметр деревьев занижаются; разорванная и склепанная мерная лента дает завышенную длину линии; простая формула срединного сечения (формула Губера) занижает объем стволов и т.д. Величину систематической ошибки можно оценить и скорректировать результат. · Двусторонние ошибки случайной величины и знака, называемые случайными ошибками, которые порождаются многочисленными факторами и присутствуют всегда, даже при очень точных измерениях. Так, на отсчет по шкале высотомера влияют освещенность, неровности поверхности земли, недостаточное равновесие маятника и т.д. Случайные ошибки установить в каждом отдельном случае трудно. К.Гаусс в начале XIX века показал, что случайные ошибки подчиняются закону нормального распределения. Случайные ошибки характеризуются рядом признаков: а) малые отклонения от «истинного» значения встречаются более часто, чем большие; б) положительные (+) и отрицательные (–) отклонения равновероятны; в) хронологическая последовательность между большими и малыми, положительными и отрицательными отклонениями не существует. · Односторонние ошибки случайной величины, называемые односторонними случайными ошибками, возникают тогда, когда случайная ошибка имеет один знак («+» или «–»). Например, глазомерный способ таксации леса дает заниженные «–» оценки запасов деревьев. Этот вид ошибок может дать неопределенная комбинация систематических и случайных ошибок. Систематические, односторонние и случайные ошибки по разному влияют на результаты измерений. Односторонние систематические ошибки постоянной величины дают смещение, значение которого увеличивается с увеличением числа измерений, т.к. ошибки аккумулируются непрерывно. Например, 20-метровая лента имеет систематическую ошибку в 2 см, т.е. при измерении длины линии в 100 м – систематическая ошибка составит: 2 см х 5 = 10 см, а 1 км – 10 х 10 = 100 см = 1 м. Средняя величина серии чисто случайных ошибок (с «+» и «–») приближается к нулю с увеличением числа наблюдений. В этом случае средняя выборка при достаточно большом числе измерений (наблюдений) является несмещенной. Таким образом, случайные ошибки взаимно погашаются. Это возможно только в том случае, если случайные ошибки являются малыми по величине и при большом числе наблюдений. Для того чтобы характеризовать случайную ошибку отдельного наблюдения (i), используют три вида оценок: средняя ошибка (Ai); стандартная ошибка (Si); вероятная ошибка (Pi). Если результат i -го измерения есть Yi, а средняя совокупности есть
Средняя ошибка вычисляется по следующей формуле:
где n – число наблюдений. Средняя ошибка используется при оценке точности инструментов и приборов. Стандартная ошибка отдельного наблюдения равна:
Стандартная ошибка – более надежная и эффективная оценка ошибки отдельного измерения или наблюдения. Вероятная ошибка
Существует соотношение в теории ошибок:
Стандартная ошибка показывает пределы ( Пример. Высота одного и того же дерева измерена высотомером Блюме-Лейсса 50 раз. Требуется провести расчеты по вышеприведенным формулам. Имеем: среднее значение высоты средняя ошибка измерений высот стандартная ошибка вероятная ошибка С вероятностью 0,68 (68 %) можно утверждать, что действительная (истинная) высота дерева находится в приделах (16,73 – 17,83). Пример. 20-метровая лента имеет стандартную ошибку Si= ±2 см. При измерении 1000 м делятся 50 измерений лентой. Стандартная ошибка арифметического среднего равна:
Стандартная ошибка всей 1000-метровой длины:
К тому же результату ведет:
Таким образом, длинна будет 999,86 – 1000,14 м с вероятностью 68%. Определение ошибок при обработке лесоводственной информации расчетным путем возможно далеко не во всех случаях и не для всех методов ее сбора и обработки, но только тогда, когда соблюдаются статистические предпосылки его сбора и обработки. Такая информация (данные) имеет право называться научно обоснованной. Диаметр дерева на высоте груди является одним из наиболее важных таксационных показателей. Это обусловлено рядом обстоятельств. 1) Диаметр – наиболее легко и точно определяемый таксационный признак; при необходимости он может измеряться у всех деревьев (сплошной перечет), тогда как другие показатели измеряются с помощью выборки. Например, для определения средней высоты проводится выборка 12 – 15 деревьев. 2) Диаметр на высоте груди обеспечивает основу для многих других вычислений: площадь сечения: объем ствола: Многие показатели (высота, товарность) статистически зависят от диаметра дерева. 3) Распределение деревьев по диаметру характеризует лесовод- ственную структуру насаждения, что важно при назначении рубок ухода, изучении роста древостоя, его сортиментации. 4) На основе измерений диаметров деревьев (перечета) определяется сумма площадей сечения древостоя, которая используется в оценке полноты и запаса насаждения. Рассмотрим ошибки измерений диаметров деревьев мерной вилкой. Инструментальные ошибки всегда являются систематическими ошибками. В процессе измерений эти систематические ошибки имеют случайное происхождение. Причины здесь могут быть разные. 1) Отклонение от горизонтали мерной вилки при измерении диаметра дерева. Ошибка в площади сечения дерева в этом случае равна:
где α – угол между мерной вилкой и горизонталью.
2) Нарушение перпендикулярности подвижной ножки к линейке мерной вилки, т.е. люфт. Получаем заниженные диаметры и отрицательную систематическую ошибку. Отклонения от перпендикулярности на 3–5 % дает погрешность в площади сечения на 5–10 % (отрицательная); 3) Ошибки измерения диаметров мерной вилкой при несоблюдении высоты 1,3 м будут следующие. Если высота измерений равна 1,20 м, то относительная ошибка составит +2,4 %. При высоте 1,25 м – относительная ошибка +1,2 %. На высоте измерений в 1,29 м относительная ошибка будет +0,24 % и т.д. Ошибки в определении диаметров и площадей сечений деревьев могут быть также вследствие ошибок перечета; ошибок наблюдения; ошибок из-за неправильной формы поперечного сечения; ошибок вследствие неправильного распределения деревьев по диаметру в пределах ступеней толщины и ошибок группировки результатов по ступеням толщины. Ошибки перечета связаны с дефектами мерной вилки и бывают самой различной величины. Ошибки наблюдения – неправильное положение мерной вилки или обмер (пропуск) повторно одного и того же дерева. Ошибки наблюдения при тщательном перечете достигают 0,3 % от площади сечения. Ошибки из-за неправильной формы сечения составляют Pg = ± 0,5 %, неравномерность распределения – Pg = ± 0,3 % – 0,8 %. Ошибки группировки – Pg = от + 1 % до – 1,5 %. Для определения ошибок вычисления площадей сечений в зависимости от точности измерения диаметра проведены специальные исследования. У опытных деревьев были измерены диаметры с точностью до 1 мм. Обозначим наибольший из них а, наименьший – b. Измерения в двух взаимно перпендикулярных направлениях обозначим как а1 и b1. По этим диаметрам вычислены площади поперечных сечений обмерных стволов. Площади поперечных сечений разделили на полоски. Вычисленные по ним площади приняты за истинные. В таблице 3.3. приведены результаты расчетов при исчислении площадей по формулам круга и эллипса.
Таблица 3.3 – Отклонения площадей поперечных сечений, вычисленных по формулам эллипса и круга, от истинных (по данным С.Е. Осетрова)
На основании данных таблицы 3.3 можно заключить, что формы поперечных сечений древесных пород в коре не представляют правильных геометрических фигур, а лишь приближаются к ним. Форму эллипса и круга, дающие близкие результаты, преувеличивают площади поперечных сечений стволов. Наибольшее преувеличение у лиственницы (+ 3,45 – 5,20 %), наименьшее у ели (+ 0,81 – 1,07 %), сосна занимает среднее положение (+ 1,77 – 2,71 %).
|

 при n измерений, то отдельное отклонение равно:
при n измерений, то отдельное отклонение равно:
 ,
, – модульная величина отклонения;
– модульная величина отклонения;
 .
. .
. ) генеральной средней переменной, находящееся за пределами (
) генеральной средней переменной, находящееся за пределами ( м (17,28±0,55);
м (17,28±0,55);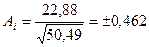 м=[0,85 Si ];
м=[0,85 Si ]; м;
м; м = [0,77 Si ].
м = [0,77 Si ]. см, т.e.
см, т.e.  .
. см
см см, т.е. (
см, т.е. ( ).
). ;
; .
. ,
,


