Объемов ствола
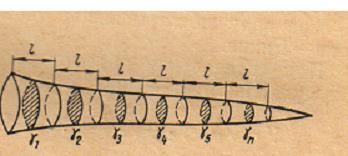
Наиболее точным способом вычисления объема ствола (Vст) является расчленение его на некоторое количество отрезков и нахождение объема ствола как суммы объемов этих отрезков (ΣVi), т.е. Здесь требуется, чтобы количество отрезков было не менее 7 – 10 штук. При научных исследованиях в молодых культурах 3-5 летнего возраста бывает деление ствола и на отрезки меньшей длины. Есть несколько способов определения объема ствола путем деления его длины (L) его на отрезки длиной l. Допустим, мы разделим ствол на «n» равных частей. Площади сечений каждого отрезка обозначим как g1, g2 … gn. Объем каждого отрезка определяем по простой формуле Смалиана, т.е. как
Объем вершины (Vв) определяем как объем конуса, т.е. Vв = Формула (5.39) называется сложной формулой Смалиана.
Рисунок 5.7 Схема разделения ствола на отрезки для определения объёма
Наиболее часто в практике научных исследований применяют сложную формулу Губера или срединных сечений. Обозначив площади сечений середины отрезков через γ имеем V = γ11 +γ2l + γ n l = l (γ1 + γ2 + … + γ n). (5.40) Известна также сложная формула Госфельда. При определении объемов отдельных отрезков по формуле Госфельда, учитывающей сечение на 1/3 длины отрезка и в верхнем отрезке, общий объем ствола будет равен:
В этой формуле сечения на одной трети отрезков Преобразовав эту формулу, получим:
При двухметровой длине отрезков для определения объема ствола по формуле Госфельда необходимо измерить диаметры в верхнем сечении каждого отрезка и на 0,67 м от их нижних сечений. В результате решения интеграла Эйлера получена следующая формула:
При определении объемов стволов или их частей по формуле Эйлера получаются меньшие ошибки, чем по формуле Ньютона – Рикке. При определении объемов отдельных отрезков по сложной формуле Ньютона – Рикке общий объем ствола будет равен:
После соответствующего преобразования формула примет такой вид:
Эта сложная формула (5.45) называется в математике формулой Симпсона, для приближенного вычисления площади интегралов. Обычно ее используют для нахождения площади, ограничиваемой параболой. При исчислении объема по формуле (5.45) надо знать диаметры для каждого отрезка в нижнем, срединном и верхнем сечениях. В Беларуси при нахождении объема ствола его часто делят на 10 частей. Это предложение проф. В.К.Захарова, о чем мы будем говорить ниже при изучении объемов растущих деревьев. В этом случае наилучшие результаты дает применение так называемой большой формулы Симпсона для приближенного решения интегралов.
где у 0, у 1, …, уn – ординаты кривой; b – а – это высота (длина) ствола (Н); n – число отрезков (обязательно четное), на которые разбита кривая.
Учитывая, что у нас n = 10, b – а = Н, то можем записать:
где Н – высота ствола; g0, g1, …, g10 – площади сечения на 0,0; 0,1;, …; 1,0 высоты ствола, Здесь di – диаметр ствола на соответствующей высоте. При проведении обмеров модельных деревьев обычно применяют сложные формулы Губера (5.41) или Смалиана (5.39), а объем вершинки определяют по формуле конуса. Хорошие результаты дает использование формулы Симпсона (5.46). Ее применение ограничивается тем, что ствол необходимо разделить на четное число частей. Это не всегда удобно, т.к. надо каждый раз вырезать новую мерную палочку или пользоваться рулеткой, что менее технологично. По этой же причине деление ствола на 10 частей не нашло широкого применения и ограничивается в основном представителями белорусских научных школ. Технологический процесс измерений более рационален, если вырезать палочку длиной 1 или 2 м, и проводить разделение всех стволов на отрезки равной длины с ее помощью.
|

 . Ствол, как правило, делится на отрезки длиной 2 м, если его высота равна 14 м и более. При меньшей высоте ствола отрезки берут длиной 1 или 0,5 м. (рисунок 5.7).
. Ствол, как правило, делится на отрезки длиной 2 м, если его высота равна 14 м и более. При меньшей высоте ствола отрезки берут длиной 1 или 0,5 м. (рисунок 5.7). . Общий объем выразится как
. Общий объем выразится как . (5.39)
. (5.39) . (5.40)
. (5.40)
 . (5.42)
. (5.42)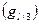 обозначены через
обозначены через  ,
,  ,
,  и т. д.
и т. д. . (5.43)
. (5.43) . (5.44)
. (5.44)
 . (5.45)
. (5.45) (5.46)
(5.46) и
и  – точки, ограничивающие
– точки, ограничивающие  ;
; ;
; 
 , (5.47)
, (5.47)



