Погрешности измерений
При измерении диаметров и высоты деревьев неизбежны ошибки, обусловливающие погрешности в определении объемов деревьев. Чтобы установить влияние погрешностей измерений на точность определения объемов деревьев, проделаем ряд расчетов. Вопрос об ошибках измерения диаметров, порождаемых непра-вильным положением вилки (непараллельностью при измерении ножек вилки) изучал румынский проф. Попеску-Зелетин. Он установил, что после длительного применения наблюдается нарушение перпендикулярности подвижной ножки к линейке мерной вилки. Вследствие этого измеряемые диаметры оказываются меньше действительных. Таким образом, получаются систематические ошибки. Все эти систематические ошибки имеют отрицательный знак. Когда подвижная ножка отклонена от перпендикулярного положения на 3 – 6 %, погрешность в определении площади сечения и объема ствола оказывается в пределах от 5,2 до 10,5 %. Поскольку рассматриваемые ошибки являются систематическими, имеющими всегда отрицательный знак, результаты измерений могут исправляться, если при этом нам известен угол. Для устранения указанных ошибок мерные вилки в процессе их применения подлежат систематической проверке. Объем цилиндра при диаметре основания D и высоте Н равен:
Если при измерении диаметра цилиндра сделана ошибка ± d, то действительный объем цилиндра будет равен
Вычтя из этого объема объем цилиндра, определяемый по формуле, получим величину погрешности в объеме обусловленную ошибкой при измерении диаметра. Величина погрешности в объеме (mV) будет такова:
Второй член полученного выражения (π/4d2H), определяющего ошибку в объеме, вследствие незначительной величины может быть исключен и ошибка в объеме принята равной:
Величину ошибки в формуле (5.48) выражают в процентах от объема цилиндра, определяемого по формуле
На основании выведенной формулы (5.49)соответственно заданной точности определения объемов может быть установлена наибольшая допустимая погрешность в измерении диаметра. Например, при диаметре 25 см и погрешности в объеме 4 % ошибка в диаметре не должна превышать
Та же формула позволяет по заданной величине ошибки в диаметре найти погрешность в объеме. Если в измерении высоты Н допущена ошибка ± h, она обусловливает следующую погрешность в объеме:
Эта погрешность в процентах составит:
Пользуясь выведенной формулой (5.50), по заданной величине погрешности в объеме можно найти наибольшую допустимую ошибку в высоте. На основе этой формулы можно решить и обратную задачу, т. е. по наибольшей ошибке в высоте, установить погрешность в объеме. Сравнивая две выведенные формулы, заключаем, что при одинаковой относительной точности измерения диаметра и высоты, когда d:D = h:H, процент погрешности в объеме будет вдвое больше при ошибке в диаметре, чем при ошибке в высоте. Ошибка в диаметре, выраженная в процентах от величины действительного диаметра, равняется:
Сравнивая эту величину с процентом погрешности в объеме, обусловленным ошибкой в диаметре pv = 200d:D, можно сделать вывод, что процент погрешности в объеме равняется двойному проценту ошибки в определении диаметра, т. е.
Если в диаметре допущена ошибка d, то площадь круга или поперечного сечения цилиндра будет иметь следующую погрешность:
Второй член полученного выражения (5.53) является весьма незначительной величиной, поэтому им можно пренебречь и погрешность в площади сечения принять равной:
Погрешность в процентах, вычисленных по отношению к площади сечения, составит:
На основании выведенной формулы можно заключить, что ошибка в диаметре влечет за собой равные проценты погрешности по объему и по площади сечения. Следовательно,
В теории ошибок доказывается, что относительная ошибка в процентах в объеме стереометрических тел равняется:
а при многих измерениях средняя величина этой ошибки определяется по формуле
При массовых измерениях бывают ошибки различной величины. У отдельных измерений могут оказаться ошибки разные по знаку. Нам необходимо определить их среднюю величину. Вывод ее затрудняется тем, что ошибки в сторону преувеличения будут компенсироваться ошибками в сторону преуменьшения, и в итоге средняя ошибка будет приближаться к нулю. Поэтому ошибки отдельных измерений можно возвести в квадрат, полученные числа сложить, затем разделить на число ошибок и из частного извлечь квадратный корень. В результате всех этих действий будет получена средняя величина ошибки, обычно называемая в вариационной статистике среднеквадратической ошибкой, которую обозначают греческой буквой «сигма» - σ. Величина среднеквадратических ошибок, допускаемых при отдельных измерениях, устанавливается по следующей формуле, известной из теории ошибок:
где n - число наблюдений. Формула (5.59) применяется, когда число наблюдений n не превышает 15. При большем числе наблюдений формула, определяющая среднеквадратическое отклонение, имеет следующий вид:
Среднеарифметическая величина, выводимая на основании отдельных наблюдений, в свою очередь имеет среднюю ошибку, определяемую по формуле:
Пользуясь этими двумя формулами (5.60, 5.61), при многократных измерениях можно определить степень точности отдельных измерений и точность средней величины, вычисленной на основе этих измерений. Согласно правилам биометрии при нормальном распределении изучаемых величин в 68 случаях из 100 ошибки не превышают среднеквадратической, в 27 случаях – удвоенной среднеквадратической и в 5 случаях – утроенной. При обмере диаметров деревья делят на ступени толщины. В пределах каждой ступени толщины существуют более мелкие деления. В ступенях толщины, близких к среднему диаметру древостоя, число деревьев, входящих в эти мелкие деления, примерно равно. В ступенях толщины, имеющих диаметр больший и меньший среднего диаметра насаждения, количество деревьев в каждом мелком делении неодинаково. Для древостоя же в целом деревья внутри каждой ступени толщины на мелкие градации по толщине распределяются в среднем равномерно. Следовательно, при разделении деревьев на ступени толщины число деревьев, диаметры которых преуменьшаются, примерно равно числу деревьев, диаметры которых преувеличиваются. При определении площадей поперечных сечений деревьев такого уравновешивания отклонений не наблюдается. Площадь поперечного сечения, как известно, равна квадрату диаметра (D 2), умноженному на постоянный коэффициент π/4. У деревьев, имеющих диаметры большие, чем половина ступени, отклонение в площадях поперечных сечений не будет компенсироваться преувеличением площадей поперечного сечения деревьев, имеющих диаметры, меньшие половины ступени толщины. Отсюда можно заключить, что учет деревьев по ступеням толщины ведет к некоторому систематическому преувеличению сумм площадей сечений. Максимальная ошибка в определении диаметра при делении деревьев по ступеням толщины равна половине ступени. Если считать, что деревья в пределах ступени толщины распределяются равномерно, средняя ошибка в определении диаметра будет равна половине максимальной. Допустим, что диаметры деревьев мы учитывали в четных сантиметрах. Следовательно, максимальная ошибка в определении диаметра будет в этом случае равна 1 см, а средняя – 0,5 см. При учете диаметров с интервалом в 4 см максимальная ошибка равняется 2 см и средняя – 1 см. При диаметре древесных стволов 20 см средние ошибки 0,5 и 1 см соответственно составляют 2,5 и 5 %. Такие ошибки влекут за собой удвоенную ошибку измерений объема, т. е. в первом случае 5 %, а во втором 10 %. Средняя величина ошибок в измерении группы деревьев определяется по ранее приведенyой формуле: (5.51)
В нашем примере они соответственно составят:
Определение объемов, как мы видим, неизбежно связано с ошибками, поэтому при вычислении объемов необходимо цифры округлять до определенного числа десятичных знаков. При таксации отдельных деревьев объем их вычисляют обычно до 0,0001 м3. При массовом учете такая точность не нужна, и объем в таблицах объёмов брёвен округляют до 0,001 или даже до 0,01 м3. Количество древесины на единице площади (1 га) обычно округляют до целых кубических метров, а при глазомерной таксации – до десятков кубометров. Цифры, характеризующие запасы лесных массивов, округляют до сотен и даже тысяч кубометров. Следует отметить общие свойства ошибок, известные из теории ошибок: малые ошибки встречаются чаще, чем большие; возможность ошибок с положительным и отрицательным знаком одинаково вероятна; с увеличением числа наблюдений сумма ошибок приближается к нулю. Ошибки делятся на систематические и случайные. Систематическими называют ошибки с одним знаком, случайными – с обоими знаками, т.е. положительным и отрицательным. Для характеристики величины ошибок чаще всего, средне-квадратическую ошибку определяют по приводившейся выше формуле (5.59).
Среднеквадратическая ошибка суммы определяется из следующего выражения:
где Среднеквадратическую ошибку разности находят по формуле:
где
Предположим, что при измерении диаметров допущена абсолютная ошибка md. Она повлечет за собой ошибку mg в площади сечения, определяемую по формуле. Сумма площадей сечений множества деревьев будет иметь следующую абсолютную ошибку:
или
Предположим, что при измерении толщины всех деревьев допущена одинаковая ошибка, равная mg. Тогда ошибка в сумме площадей сечения всех деревьев будет следующей:
Ошибка в площади сечения, выраженная в процентах, окажется такой:
Сумму площадей сечений (∑ g) заменим произведением площади сечения среднего дерева g на общее число деревьев N, составляющих данное множество. Тогда будем иметь:
Подставив (π/4) D2N вместо ∑ g в ранее приведенное выражение, в конечном итоге получаем следующую упрощенную формулу:
Согласно полученной формуле для приближенного вычисления ошибки надо удвоенную ошибку в измерении среднего дерева разделить на квадратный корень из общего количества обмеренных деревьев. Этот теоретический расчет величины средних ошибок подтверждается опытными данными, полученными А. С. Матвеевым-Мотиным. Им было заложено восемь пробных площадей и для каждой из них вычислены суммы площадей сечений при округлении диаметров до 1, 2, 4 и 5 см. Несмотря на разную дробность округления, или разную величину ошибок, допускаемых в измерении диаметров отдельных деревьев, суммы площадей сечений оказались близки между собой. На всех восьми пробных площадях отклонение в суммах площадей сечений не превышало +0,8 %. Аналогичные данные получаются и при вычислении ошибок по формуле (5.68). Автором учебного пособия также проведена проверка точности определения суммы площадей сечения при проведении перечётов по ступеням толщины в1, 2, 4см.Результаты подтвердили вышеприведенные данные при среднем диаметре 16см и более. В данном случае важно, чтобы количество разрядов (ступеней тплщины) в нашей статистической совокупности было в пределах от 7-8 до 12-16. Таким образом, можно заключить, что при учете отдельных деревьев необходимо измерять диаметры как можно точнее, в противном случае при вычислении объема деревьев получатся существенные ошибки. При массовом же учете леса в измерении диаметров отдельных деревьев допустимы значительные округления, которые существенного влияния на суммарный результат не окажут, так как разные знаки взаимно уничтожаются. М. Продан в книге «Messung der Waldbestände» («Измерение насаждений») подробно останавливается на установлении ошибок при определении диаметров и площадей сечений. Он указывает, что эти ошибки состоят из ошибок перечета; так называемых ошибок наблюдения; ошибок из-за неправильной формы поперечного сечения; ошибок, порождаемых неравномерным распределением деревьев в пределах ступеней толщины, и ошибок округления. Ошибки перечета связаны с дефектами мерной вилки. Они могут быть самой различной величины. Ошибки наблюдения возникают от неправильного положения вилки при перечете и субъективных ошибок (обмера одного дерева 2 раза или его пропуска). При тщательном перечете, по мнению Продана, ошибки наблюдения достигают 0,3 % от площади сечения. Ошибки из-за неправильной формы ствола составляют ± 0,5 % от площади сечения. Ошибки, порождаемые неравномерным распределением деревьев в пределах ступеней толщины, зависят от характера распределения деревьев в данной ступени. Они составляют в более мелких ступенях толщины ± 0,1 – 0,3 %, в более крупных ± 0,03 – 0,8 % от площади сечения деревьев, входящих в эту ступень. Ошибки округления колеблются от – 1,5% до + 1 %. Данные М. Продана совпадают с результатами исследований, проводившихся в СССР А.Г. Мошкалевым и другими учеными.
|

 .
. .
.
 (5.48)
(5.48) ;
; (5.49)
(5.49)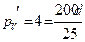 ;
;  .
.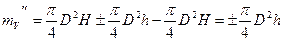
 ;
;  . (5.50)
. (5.50) , (5.51)
, (5.51) . (5.52)
. (5.52) (5.53)
(5.53) (5.54)
(5.54) ;
;  (5.55)
(5.55)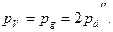 (5.56)
(5.56) , (5.57)
, (5.57) . (5.58)
. (5.58) (5.59)
(5.59) - сумма квадратов отклонений отдельных измерений от их среднеарифметической величины;
- сумма квадратов отклонений отдельных измерений от их среднеарифметической величины; . (5.60)
. (5.60)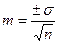 (5.61)
(5.61) и
и 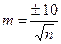 .
. , (5.62)
, (5.62) – среднеквадратические ошибки отдельных слагаемых.
– среднеквадратические ошибки отдельных слагаемых. , (5.63)
, (5.63)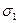 – среднеквадратическая ошибка уменьшаемого;
– среднеквадратическая ошибка уменьшаемого; – среднеквадратическая ошибка вычитаемого.
– среднеквадратическая ошибка вычитаемого. ,
,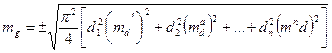 . (5.64)
. (5.64)
 . (5.65)
. (5.65) . (5.66)
. (5.66) . (5.67)
. (5.67) =
= 
 . (5.68)
. (5.68)


