Поперечная форма древесного ствола
Дерево состоит из корней, ствола, ветвей и сучьев, образующих крону. Наиболее ценной частью дерева, на долю которой приходится в среднем 60 – 85 % его объема, является ствол. Поэтому определение объема ствола составляет одну из главных задач лесной таксации. Древесный ствол, как и отдельные его части, имеет некоторое сходство с правильными стереометрическими телами. Поэтому при определении объемов растущих и срубленных деревьев или частей ствола могут быть применимы законы и правила стереометрии. Форма древесных стволов весьма разнообразна. У деревьев, выросших в густом лесу, стволы более правильной формы, у одиночно растущих деревьев – обычно неправильной, при этом у них сильно развита крона (рисунок 5.2).
Рисунок 5.2 Деревья, выросшие в насаждении (слева) и на свободе
Поперечные срезы древесных стволов, или, как принято их называть, поперечные сечения, по форме напоминают круги или эллипсы. Исследования показали, что у хвойных пород взаимно перпендикулярные диаметры в нижней трети ствола в среднем различаются на 3,7 %, а в средней части ствола – на 3,1 %. Форму поперечных сечений древесных стволов уже более 100 лет назад детально изучали С.Е. Осетров и проф. В.Я. Добровлянский. С.Е. Осетров исследовал форму поперечных сечений (в коре), расположенных на высоте 1,3 м от шейки корня, у 27 еловых, 13 сосновых и 10 лиственных деревьев. Контуры срезов стволов были перенесены на бумагу и площади их исчислены геометрическим способом. На рисунке 5.3 показан контур поперечного сечения ствола, разделенный на секторы поперечными линиями. Каждый сектор разбит в свою очередь на полоски одной шириной 2 см. посередине каждой полоски проведена пунктирная линия, обозначенная буквой К с соответствующим индексом.
Рисунок 5.3 Схема измерения площади поперечного сечения ствола
Площади полосок р определены по формуле Симпсона, применяемой в математике при приближенном решении интегралов:
Площадь всего сектора Р1 будет равна сумме площадей полосок:
Площадь поперечного сечения ствола будет равна сумме площадей трех секторов и четырех треугольников: Робщ = Р1+Р2+Р3+ 4∆. (5.5) У исследованных деревьев обмерены были с точностью до 1 мм наибольший α, наименьший b и два взаимно перпендикулярных α1 и b 1 диаметра. По этим диаметрам были вычислены площади поперечных сечений обмеренных стволов. Площади поперечных сечений, найденные по формуле (5.4), требующей разделения срезов на полоски, приняты за истинные, а отклонения площадей сечений, вычисленных по формулам круга и эллипса, выраженные в процентах. Полученные результаты приведены в таблице 5.1. На основании данных таблицы 5.1 можно заключить, что формы поперечных сечений древесных пород в коре не представляют правильных геометрических фигур, а лишь приближаются к ним. Формулы эллипса и круга преувеличивают площади поперечных сечений стволов. Наибольшее преувеличение (3,45 – 5,25%) оказалось у лиственницы, сосна занимает среднее положение (1,77 – 2,71 %), наименьшее преувеличение дала ель (0,81 – 1,07 %). Формулы эллипса и круга дают близкие результаты.
Таблица 5.1 – Отклонения площадей поперечных сечений, вычисленных по формулам эллипса и круга, от истинных (по данным С.Е. Осетрова)
Проф. В.Я. Добровлянский исследовал девять сосновых стволов, разрезав их на части длиной 2,13 м. Каждый срез в коре и без коры он переносил на кальку и площади их вычислял планиметром. Результаты его исследований, дополнительно обработанные проф. А.В. Тюриным, приведены в таблице 5.2.
Таблица 5.2 – Отклонения площадей поперечных сечений, вычисленных по формуле эллипса, от истинных
Наиболее близкие к истинным получаются площади сечений, вычисленные по формуле эллипса, определяемой по наибольшему и наименьшему диаметрам. Менее точные результаты получаются при определении площадей эллипсов по двум взаимно перпендикулярным диаметрам. Наибольшее приближение площадей эллипсов наблюдается в средней (10,65 м) и верхней (21,3 м) частях стволов. Формула эллипса преувеличивает площадь сечения в коре нижней части ствола (2,13 м), что объясняется неровностями и трещинами коры в этой части ствола. Поперечные сечения стволов сосны без коры во всех частях ствола близки к площади эллипсов. Сопоставление данных С.Е. Осетрова и В.Я. Добровлянского показывает, что при определении поперечных сечений нижней части ствола по формулам круга и эллипса погрешность исчисления возрастает с увеличением высоты измерения. В среднем она равна 1 %. У деревьев с толстой корой эта разница достигает 2 – 3 %, а с очень толстой – 4 – 5 %. При вычислении площадей поперечных сечений окоренных стволов формулы круга и эллипса дают для любого сечения по всей высоте ствола преувеличение на 0,5 – 1 %. В широкой таксационной практике ошибки, не превышающие приведенных выше, считаются неизбежными. Поэтому площади поперечных сечений находят по формуле круга, обеспечивающей точность до 3 %. Площади кругов по сравнению с эллипсами дают незначительное превышение, вытекающее из следующего теоретического расчета:
При равенстве α; и b площади эллипса и круга равны. По мере увеличения разницы между величинами α; и b расхождения в площадях увеличиваются.. Таким образом, мы видим, что определение площади поперечного сечения по формуле круга не приводит к значимым ошибкам. Поэтому в практике поперечные площади сечений деревьев определяют как площадь круга. При проведении научных исследований, чаще всего, измеряют два противоположных диаметра дерева и выводят среднее значение. Еще более точные результаты получают, обмеряя окружность ствола рулеткой. Этот метод, как правило, используют при работе на постоянных пробных площадях, которые именуют стационарами. Разница в диаметрах отдельных деревьев в древостое, которые измеряют в одном направлении, например, север-юг, носит случайный характер. Это значит, что отклонения от среднего значения, вычисленного по измерениям диаметров в двух взаимно перпендикулярных направлениях, со знаком (+) и (-) примерно равны и взаимно погашаются. Поэтому в практике диаметры деревьев измеряют в одном выбранном направлении, что удовлетворяет требования к точности определения объемов ствола.
|



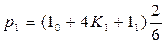 , (5.1)
, (5.1) , (5.2)
, (5.2) . (5.3)
. (5.3) (5.4)
(5.4) на высоте от пня, м
на высоте от пня, м
 на высоте от пня, м
на высоте от пня, м
 (5.6)
(5.6)


